Lab 1:
Fast and Spurious

The questions below are due on Friday February 21, 2025; 10:00:00 AM.
 
You are not logged in.

Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.
You are viewing the 6.3100 Spring 2025 web site. Please note that information on this page may change throughout the semester, please check back frequently.

Quick Reference

Parameter Indices to use in the serial plotter "Send" window

Links

  • Software to install is described here.
  • Build instructions are here.
  • Sketch for this lab is here.

Task Summary

Week A

  1. FIND A PARTNER.
  2. Install Software.
  3. Build and Test the Speed Control Hardware (checkoff 1).
  4. Determine the roles of the ticksperupdate, kff, kp, repeats, freq, and amp, and DisturbA (checkoff 2).

Week B

  1. Extract coefficients from data for a 1st-order difference equation model.
  2. Use model to inter-relate gains, update period, and stability. Compare with experiments (checkoff 3).
  3. Investigate how gains effect tracking error and disturbance rejection, design controller (checkoff 4).
  4. Collect experimental data for the postlab using various values of ticksperestimeate (as screenshots) (Checkoff 5).

Safety First

Please read the EECS Lab Safety instructions.

  • We will be building and debugging electrical systems. While everything we do in this subject is low-voltage, you should never modify or even touch a circuit without turning off its power.
  • We will be using small but very high speed motors. If our systems go unstable, parts can fly off in any direction. Please wear safety goggles when using the high-speed motors with spinning propellers.
Please sign the EECS Lab Safety form now! You will not be allowed to work in the lab (38-545) and get a grade in this subject unless you indicate that you have reviewed the safety instructions by signing the form.

Introduction

The goal of this lab is to control the speed of a motor, while learning about

  1. Control system modeling,
  2. Feedback and Stability,
  3. Sample Rate Effects,
  4. Steady-state and Dynamic Tracking,
  5. Insensitivity to Disturbances and uncertainty,

As you will see, the issues associated with control will be obvious and direct, but the issues associated with modeling will be both pervasive and, unfortunately, subtle.

After constructing and testing the speed control system, you will collect data from which to calibrate a first-order difference equation model for the relationship between the Teensy-sketch-generated motor command and the measured motor speed. You will then use this model to make reasonably good predictions about the interactions between sample rates, controller gains, stability, tracking errors, and disturbance insensitivity.

Then, in preparation for the post-lab, you will collect another data set, one specifically designed to expose inaccuracies in the first-order model. As part of the post-lab, you will derive, calibrate, and analyze an improved second-order model, and see if its predictions are better (spoiler alert, sometimes they are).

The take-away about modeling from this lab and post-lab is NOT (we repeat, NOT) that one model is good and the other is bad. As you will see in lab, a first-order model is accurate enough (and simple enough) to answer questions about the interaction between sample rate and stability, or feedback gain and disturbance rejection. But as you will see in the postlab, you'll need a second order model to accurately predict the stability limits on gain, or to predict waveforms near the stability limit.

So, what is the take-away from this lab and postlab about modeling? A good model is usually the simplest model that correctly answers your questions.

Installation and Construction

We use the Arduino IDE 2.3.2 software (with modifications and a 6.310 specific library) to communicate with, program, and plot results from our 6.310 controller board (based on the Teensy 4.1 microcontroller). Throughout the term, you will be using this software-board combination, along with lab-specific hardware, to design and experiment with algorithms that control motor speed, rotating arm position, and even magnetic levitation.

Put Together Your Lab Kit. Staff will help you find parts.

Install the Software as described here.

Build and Test the Speed Control Hardware as described in the speed assembly guide here.

Checkoff 1:

After you have carefully followed ALL the steps in the step-by-step assembly guide, demonstrate your working speed control hardware.

  • Demonstrate the operation of your motor by plotting results using mode 0. Describe what is plotted on the horizontal and vertical axes. (Hint: In mode 0, the Teensy samples the optical sensor once every 66.6\museconds.) Describe a method for determining motor speed from this plot. What is the speed indicated by the plot?

  • Change the teensy sketch to mode 1 (line 13), reupload, and reopen the serial plotter. In mode 1, the speed of the motor is controlled by a feedback system, and the measured speed, desired speed, and motor command are being plotted. The speeds are in rotations per second (RPS) minus the nominal speed (set to 15 in the Teensy sketch). The potentiometer you attached to the controller sets a nominal motor command, what maximum offset from the nominal speed can you achieve by rotating the potentiometer?

  • Use the send window in the serial plotter (DO NOT MODIFY THE SKETCH!) by setting the desired speed to toggle between 14 RPS and 16 RPS every five seconds by first typing 6 1 (followed by return) in the send window, to set the input amplitude to one, and then typing 5 0.1 (followed by return) to set the frequency to 0.1 or the period to 10 seconds. When using the send window, the first number is an integer and is the parameter index (a list of integer-parameter pairs is at the top of every lab) and the second number is the parameter value. Explain what is changing in your plots.

  • Try modifying the feedback gain by setting Kp using the send window. A feedback term is added to the nominal command when Kp is non-zero, and is proportional to the difference between the desired and measured motor speeds, scaled by K_p. Use the send window to try different values of Kp, be sure to try 1, 0.1, and 0.0. What value of Kp is too large, and why?

  • Try setting a non-zero disturbance by setting the value of DisturbA (on line 14 of sketch) to 0.3, reuploading and reopening the plotter, and using the send window to reset the input amplitude to one and the oscillation frequency to 0.1. Then try increasing the feedback gain, starting from 0.1 and doubling (to 0.2, 0.4, ...). What is the effect of gain on the behavior of the measured motor speed?

Structure of the Control System

The following block diagram illustrates the structure of the speed control system that we will develop.

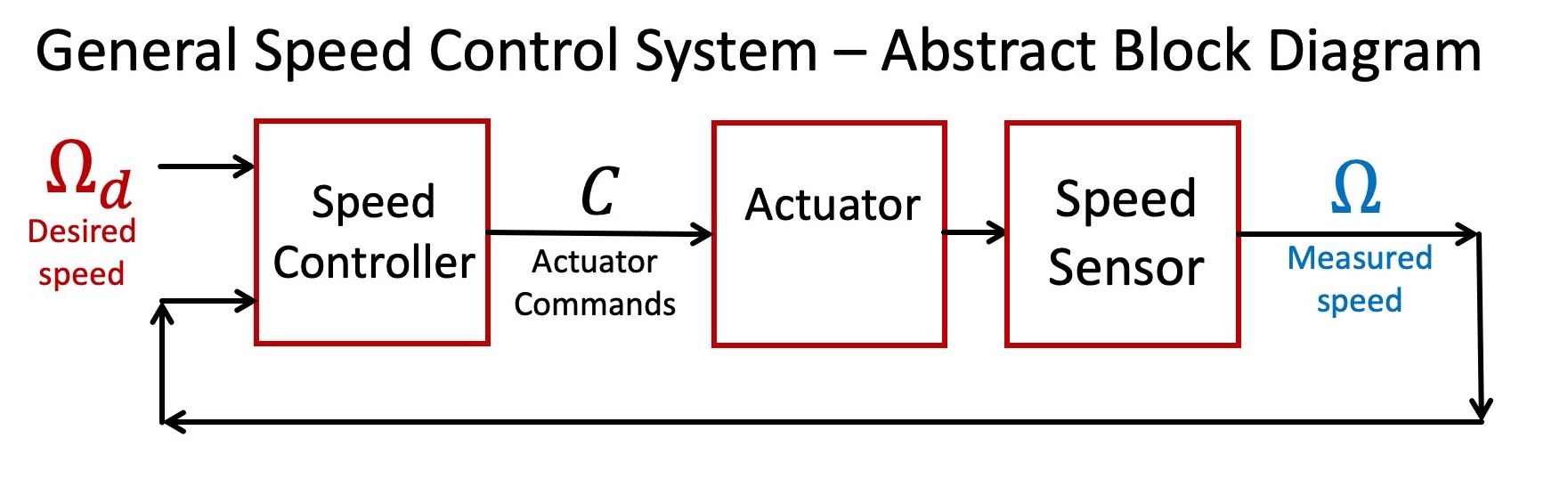
As this diagram suggests, controlling the rotation speed of a spinning object requires three interconnected functions. Foremost of the three is an actuator that can be commanded to either accelerate or decelerate the object. Second, one needs a sensor to verify the object's speed. And thirdly, the focus of much of this class, one must design a controller that can determine effective actuator commands given the desired and measured speeds of the object.

Perturbations from Nominal

As you may have noticed when testing your speed-controlled motor system, there is a nominal speed of 15 rotations/second (15 RPS), and an associated nominal actuator command. All the other speeds and commands are offsets to these nominal values, so our system is more precisely described by the abstract diagram below. We formulated our speed control problem in terms of perturbations from nominal values partly because it is a natural fit to the common control problem, maintaining constant speed (think automobile cruise control). But more importantly for our purposes, relationships between perturbations are likely to be more linear, and therefore more easily modeled. And good models, as we shall see thoughout the term, are essential precursers to designing good controllers.

Abstracting from Structure

Below is a functional block diagram of our speed control system, based on its physical structures. What should be immediately clear is that the functional block diagram looks nothing like the abstract block diagrams above. For example, is the motor the actuator? Or is it the motor plus the H-Bridge drivers? Also, the combination of the white eight-bladed encoder and the optical sensor does not produce rotation speed, it produces a signal from which the speed can be deduced. So does the combination really form the sensor in our abstract model?

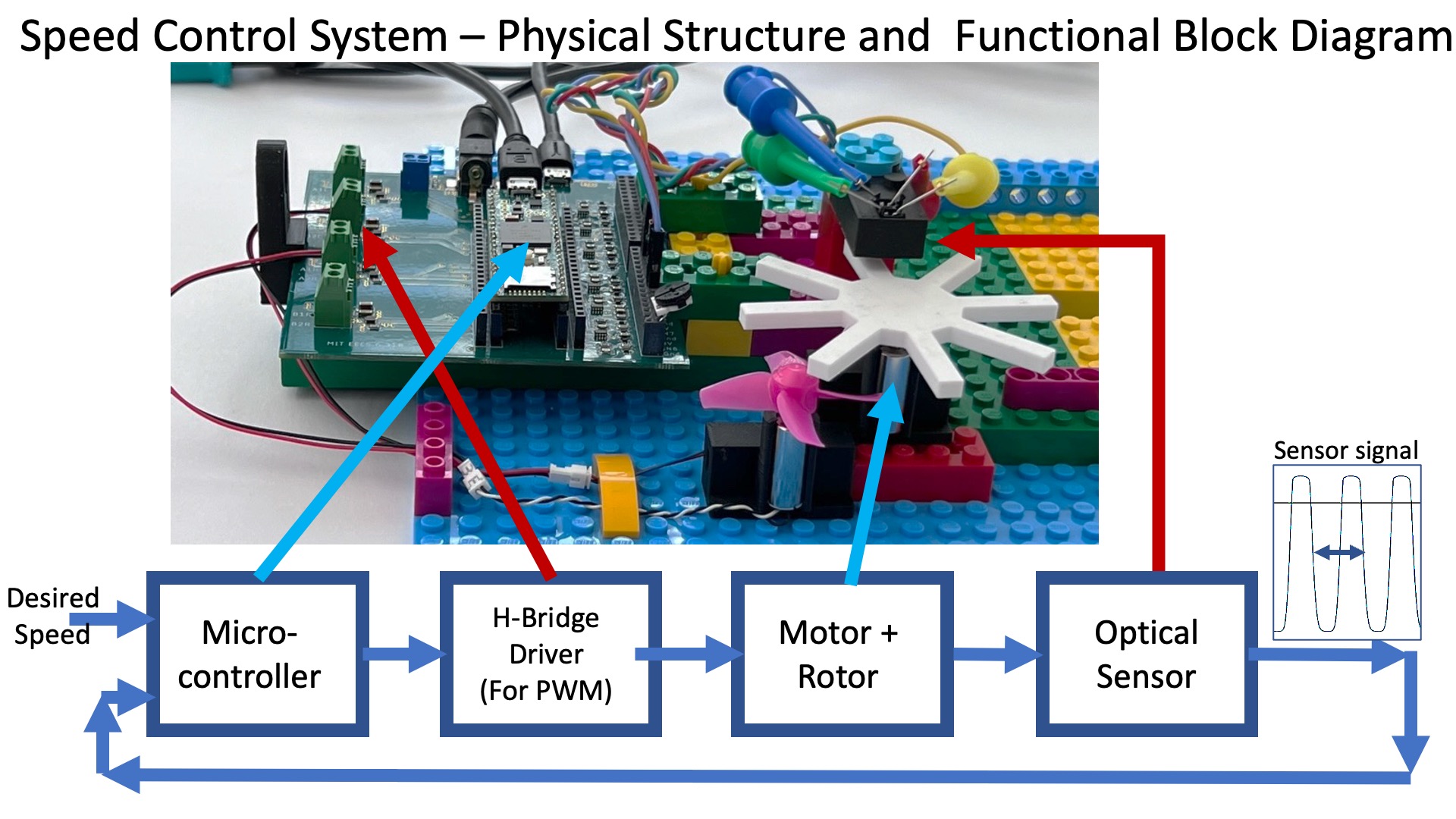
Whether the problem is software or hardware or some combination of the two, finding a good abstract model is often the central challenge in any engineering design. As we noted in the introduction, a good model has enough detail to accurately assess design tradeoffs, yet is simple enough to reveal alternative strategies. But, how does one find a model good enough to answer one's questions, if one needs the model to determine what questions to ask? And how does one find a model that reveals strategies one does not yet know?

Modeling, it is impossible to teach, but fortunately, not impossible to learn.

Connecting Structures and Abstractions

In the case of our speed control system, we can extract an abstract model like the one above provided we ignore the structural boundaries. The speed sensor is a combination of the white eight-bladed encoder, the optical sensor, and the function getSpeed in the Teensy sketch (which converts the time between falling edges in the optical sensor output into speed estimates, see the next section). The actuator in the abstract diagram is a combination of the function hbridgeBipolar in the Teensy sketch (which converts a motor command into a pulse-width-modulated signal), the h-bridge driver, and the motor connected to the white encoder.

We summarize the connection between abstract model and structural implementation in the figure below.

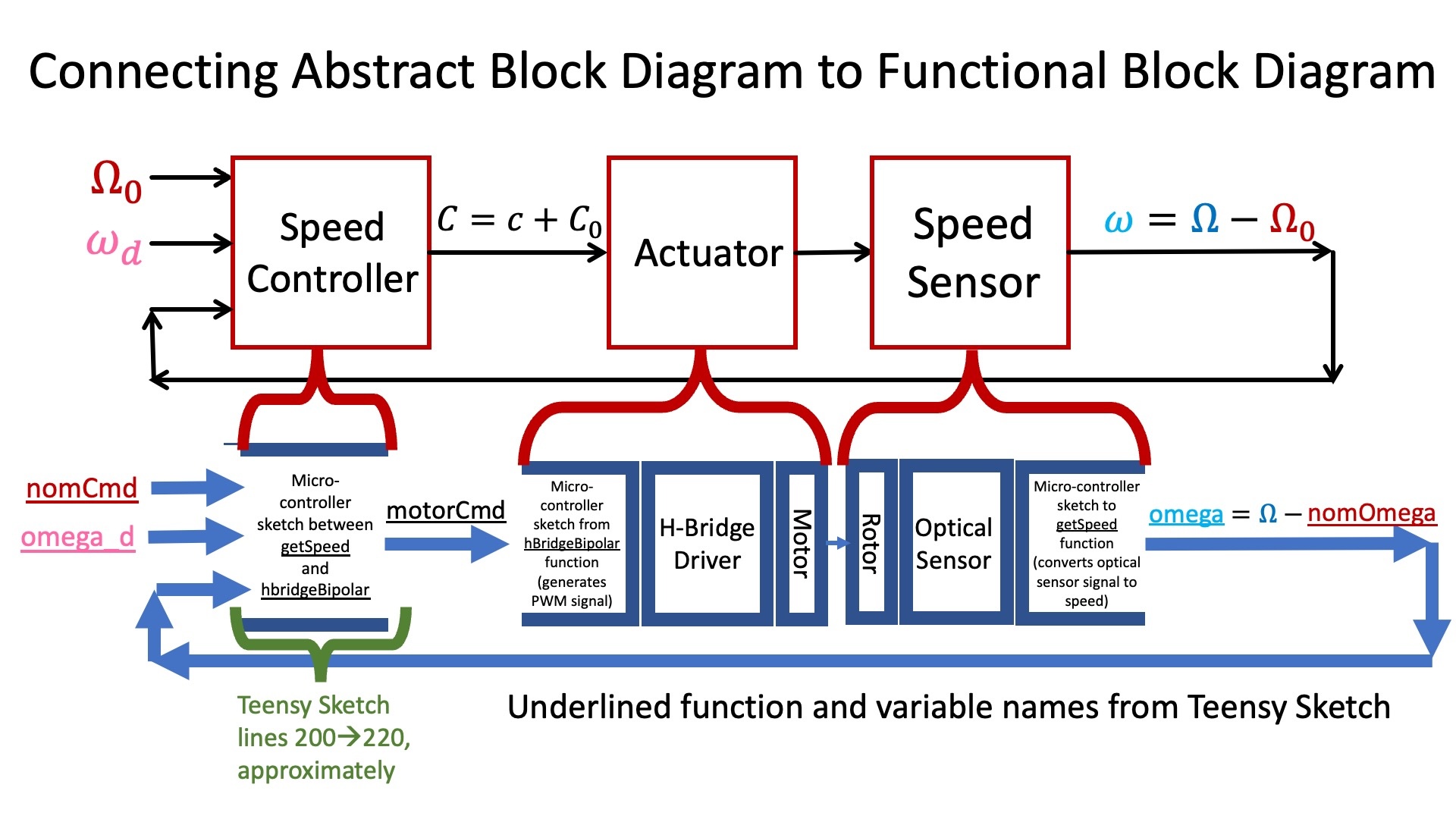
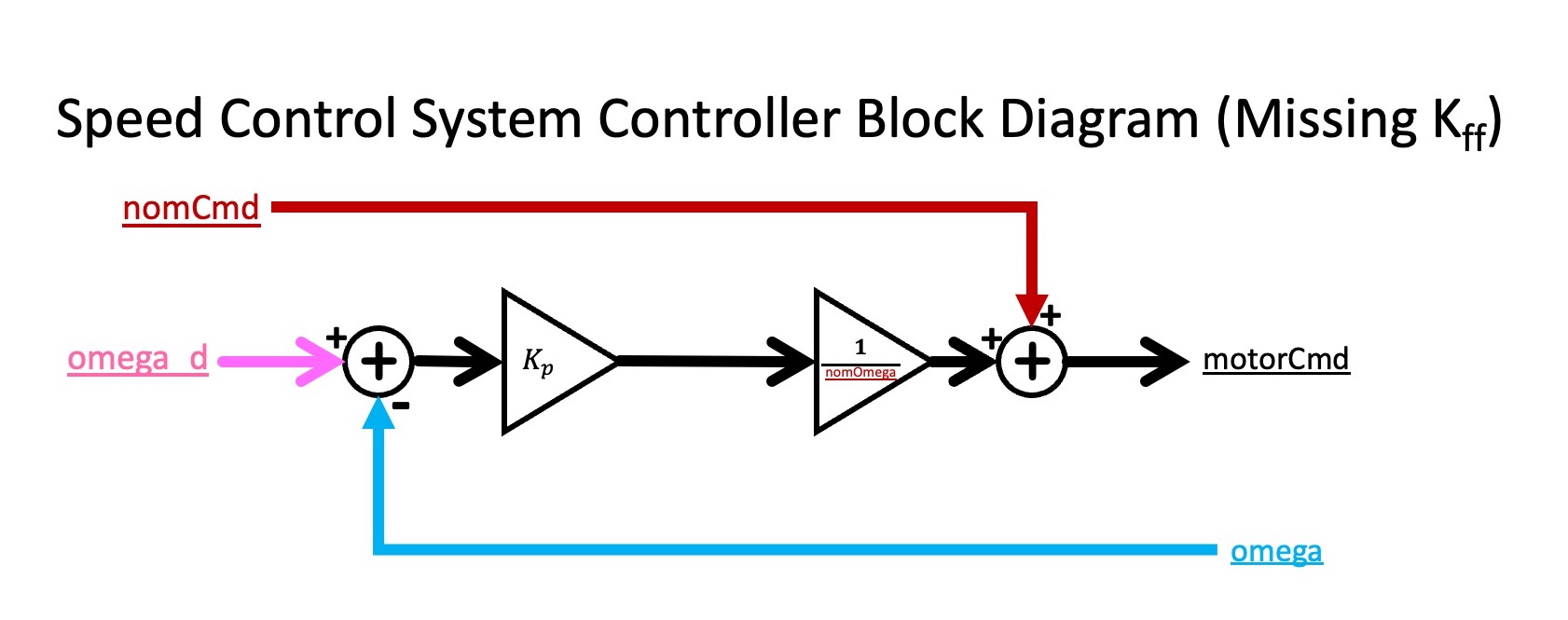
The Controller Block

As we can see from the figure in the previous subsection, there is a small part of the Teensy sketch that corresponds to the speed-controller block in the abstract block diagram. The actuator command, motorCmd in the sketch, is computed from the nominal command, nomCmd in the sketch, the desired perturbation in motor speed, omega_d in the sketch, and the measured perturbation in motor speed, omega in the sketch. To make the meaning of omega and omega_d clearer, consider the example plot below. The plot was generated by running the speed control system in control mode (MODE 1), with omega_d set to be a unit amplitude square wave, the controller gain kff set to 0.025, and the square wave frequency set to \frac{1}{25}.

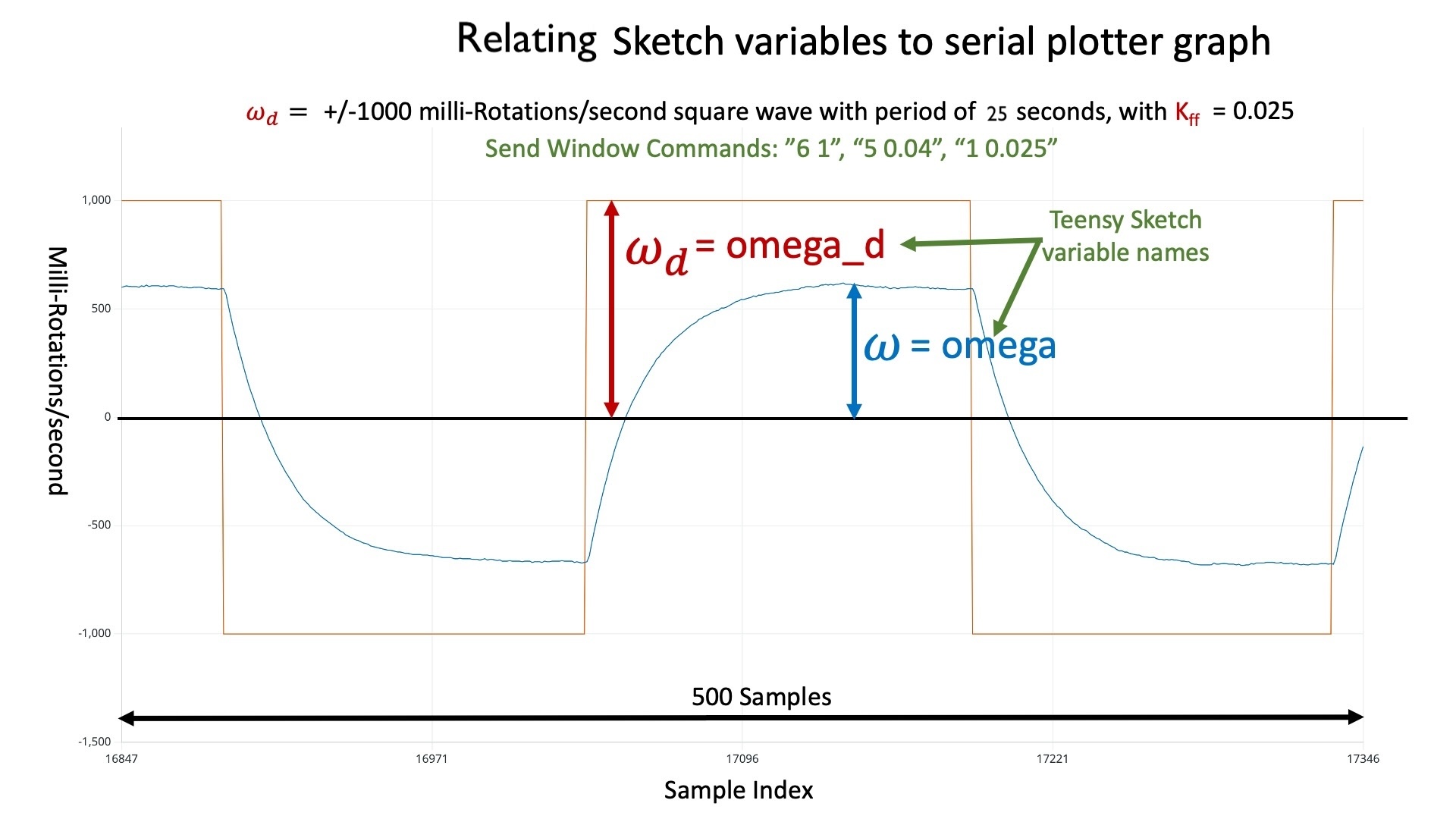
Below we show an incomplete block diagram for the controller, showing how the motor command is computed from the desired and measured motor speeds, as well as the nominal command (which is just added in). The block diagram shows how K_p, the proportional feedback gain, effects the motor command, but does not show the effect of K_{ff}. We will consider adding K_{ff} later in the lab.

Sensing Speed

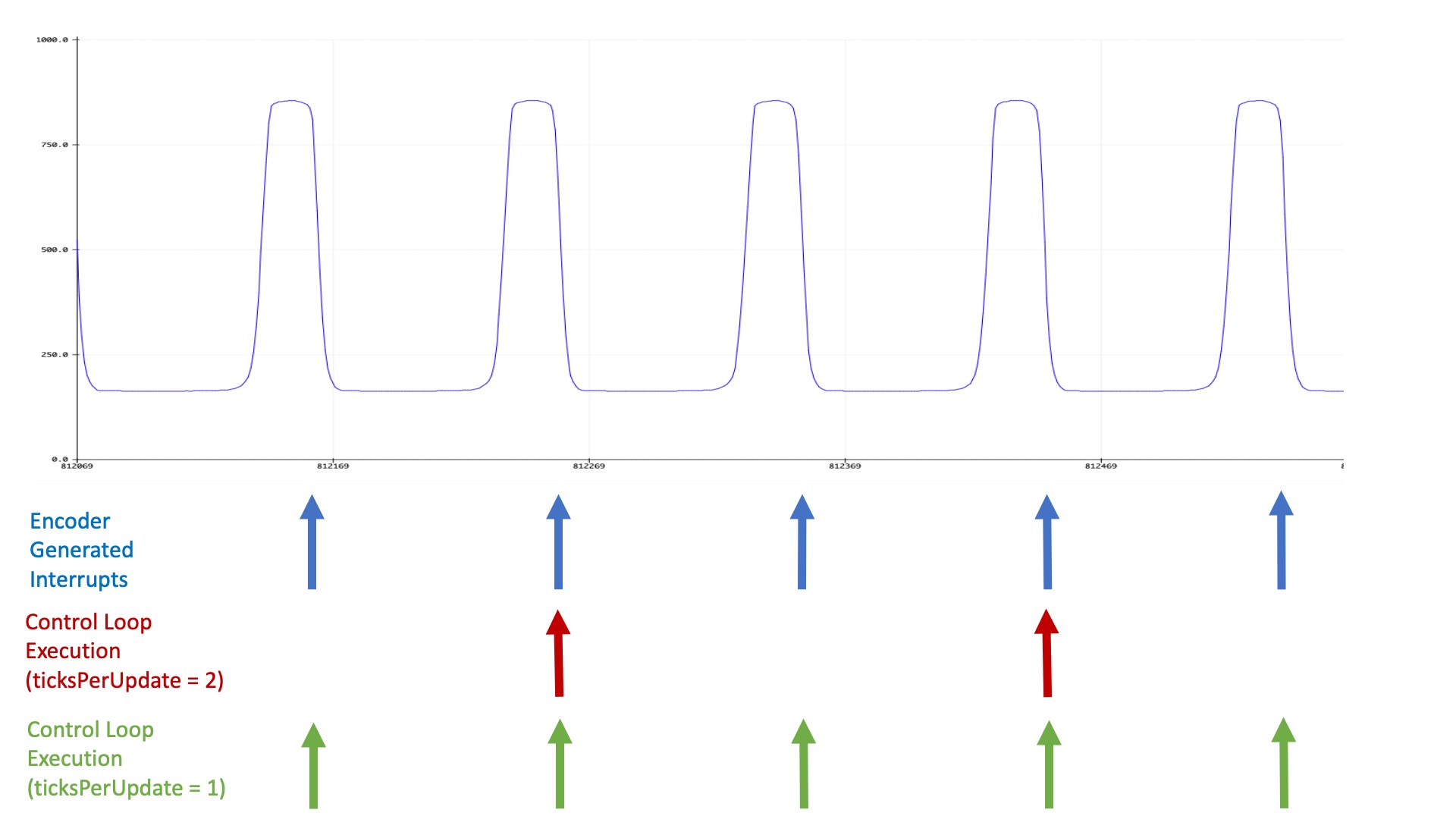
The optical sensor generates a pulse every time a white encoder blade passes underneath it. More specifically, the blade reflects the infrared light from the led on one side of the sensor to the optotransistor on the other side of the sensor, and when bombarded with infrared light, the optotransistor turns "on". The "on" transistor effectively "pulls-up" the IN5 input on the 6.310 controller board, increasing the voltage from close to zero to nearly three volts. Once the encoder blade passes out from under the sensor, the optotransistor turns "off", the IN5 voltage is pulled back down to zero by a resistor ground (see the schematic in the assembly guide).

The negative change in the voltage on IN5 "interrupts" the microcontroller, which determines the time since the last negative change, and computes the motor speed.

The signal generated by the optical sensor circuit is plotted below (notice the y-axis is normalized, so that 1000 corresponds to three volts), along with a diagram showing when interrupts are triggered on the Teensy, as well as when a control loop (which updates the motor command) executes. As the diagram should make clear, interrupts are generated every time an encoder blade passes under the optical sensor (eight times per rotation for our eight-bladed encoder), but the control loop only runs every m^{th} interrupt, where m is the setting of ticksperupdate (which you change from the serial plotter send window, by typing, e.g. "0 4" to set ticks per update to 4). Note that when ticksperupdate is zero, m is set to the maximum value of 8.

Checkoff 2:

Set the disturbance amplitude to back to zero, reupload the sketch, and reopen the serial plotter. Reset the input amplitude to 1 and the oscillation frequency to 0.1 using the send window, and then experiment with modifying ticksperupdate from 1 to 8.

  • For what value of ticksperupdate is thenoise'' in the speed measurement largest? Can you explain why the noise level depends on ticksperupdate?

  • Does changing ticksperupdate change the effect of K_p? Show plots to demonstrate your result.

  • Remodify sketch to set the disturbance amplitude back to 0.3, reupload, reset the input amplitude to 1 and the period to 0.1. What combination of ticksperupdate and Kp values gives you the best match between desired and measured speed?

STOP HERE FOR THE FIRST WEEK!!!!

Difference Equation Modeling.

As we saw in class we can construct a first-order difference equation model for our feedback control system, and use the model to design a good controller. In general, we approach modeling in two steps:

  1. Apply a few physical prinicples to determine a parameterized form of the model and,
  2. Extract the parameter values from the results of carefully-chosen experiments.

Model Form

Recall that when first experimenting with the speed control system, we turned a small potentiometer to adjust a nominal motor command, C_0 (nomCmd in the Teensy sketch), to set a nominal motor speed, \Omega_0 (nomOmega in the sketch). We then perturbed the motor command (e.g. by setting non-zero feedback or feed-forward gains) and measured the perturbation in motor speed. In order to model our system more precisely, we will use lower case letters to denote perturbations from nominal,

c[n] = C[n] - C_0 \;\;\; \omega[n] = \Omega[n] - \Omega_0 \;\;\; \omega_d[n] = \Omega_d[n] - \Omega_0
where c[n] (corresponding to cmd in the sketch) is the measured perturbation in motor command, \omega[n] (corresponding to omega in the sketch) is the perturbation in measured motor speed, and \omega_d[n] (corresponding to omega_d in the sketch) is the desired perturbation in motor speed.

To start, changes in motor speed can be related to motor acceleration, \alpha, by

\omega[n] \approx \omega[n-1] + \Delta T \alpha[n-1],
where \Delta T is the time between speed samples. The motor is accelerated and decelerated by perturbations in two torques, one proportional to perturbations in motor command (which changes the motor current) and the other proportional to motor speed (due to friction and air resistance). Denoting \gamma and \beta as the proportionality constants for command and friction respectively,
\omega[n] \approx \omega[n-1] + \Delta T \cdot \left(\gamma c[n-1] - \beta \omega[n-1]\right).
Now, we have a form for the model and can start to design the experiments needed to determine \beta and \gamma for our particular speed control system (these are not precision motors, don't expect to get the same answers as your labmates).

Note: since the sample period is dependent on the motor speed, and the motor speed is being perturbed, we are explicitly ignoring the perturbations in \Delta T. We will assume \Delta T \approx \frac{1}{\Omega_0} (assuming the motor speed is in units of RPS).

Parameter Calibration

One way to generate responses from which to calibrate the linearized model is to use the AMP index in the send window to set the maximum value of omega_d to ten percent of the nominal speed (nominal speed = 15 RPS, so we want to set amp = 1.5 using the sender window), then use the KFF index to set K_{ff} so that omega reaches a steady-state that matches omega_d. You will need to set the input frequency low enough so that the motor speed settles between transitions (perhaps 0.05 hertz or ten seconds between transitions, using the send window and the FREQ index). The approach is illustrated in the following figure.

For the above senario, and in steady-state, \omega[n] = \omega[n-1]= \omega_d[n]. Since

c[n] = K_{ff}*\omega_d[n],
there is a lot of fortuitous cancellation, yielding a simple relation between our unknown parametes, \beta and \gamma.

You can derive a second relation involving \beta and \gamma by examining the immediate (rather than steady-state) behavior of the perturbed motor speed, \omega[n], in response to the step changes in \omega_d[n]. And the analysis of \omega[n] dynamic behavior will simplify if you exploit the fact that the system is linear, and that both \omega and \omega_d are in steady-state before the step change and eventually in a different steady-state afterwards.

See additional notes on this analysis in the notes from lecture 2b.

NOTE: You can stop the plot by clicking on the run-stop icon in the plotter, and when stopped, you can move the cursor to any plot to find its x-y values.

Testing Your Model

For the feedback case, the c[n] for your system becomes,

c[n] = K_p*(\omega_d[n] - \omega[n])
and the system will only be stable for a certain range of K_p. You should be able to derive, analytically, the range of stable K_p's given your calibrated values of \gamma and \beta.

Test your analysis against experiment by using the same values for the AMP and FREQ indices as you used for model calibration, setting K_{ff} to zero, and then slowly increasing K_p (starting with K_p=0) and watching the step responses. Determine when your system goes unstable and see if your experiments match your analytic predictions from your calibrated model.

Determine the Parameters for Your Motor

There are two coefficients to estimate (\beta and \gamma), and two types of information in your measured step responses, how fast the measured speed changes and the change in steady-state value.

For this checkoff, determine \beta and \gamma for your system, and test how well your model predicts the onset of instability (with ticksperupdate set to 8).

Enter your value of \beta:  

Enter your value of \gamma:  

Checkoff 3:

  • What values did you determine for \beta and \gamma, and how did you find them?

  • Calculate the maximum value of K_p for which the mathematical model of the system is stable and compare it to the maximum value of K_p for which the physical system is stable. How well do they match?

Investigate Sample Time and Disturbances

With the input amplitude set to one and the frequency set to 0.2, use the send window to set the ticksperupdate to 4, then 2 and then 1. How will you change \Delta T in your difference equation model to reflect these changes? For each value of ticksperupdate, find the maximum value of K_p for which the system is stable, and see if your experiments match your updated models.

In the figure below, we plot the behavior of our system as we altered the input amplitude and the disturbance (with a moderate value for K_p). For the first third of the plotted interval, both the disturbance and the input were on, for the second third, only the disturbance was on, and for the last third, only the input was on. What property of the system is this plot demonstrating?

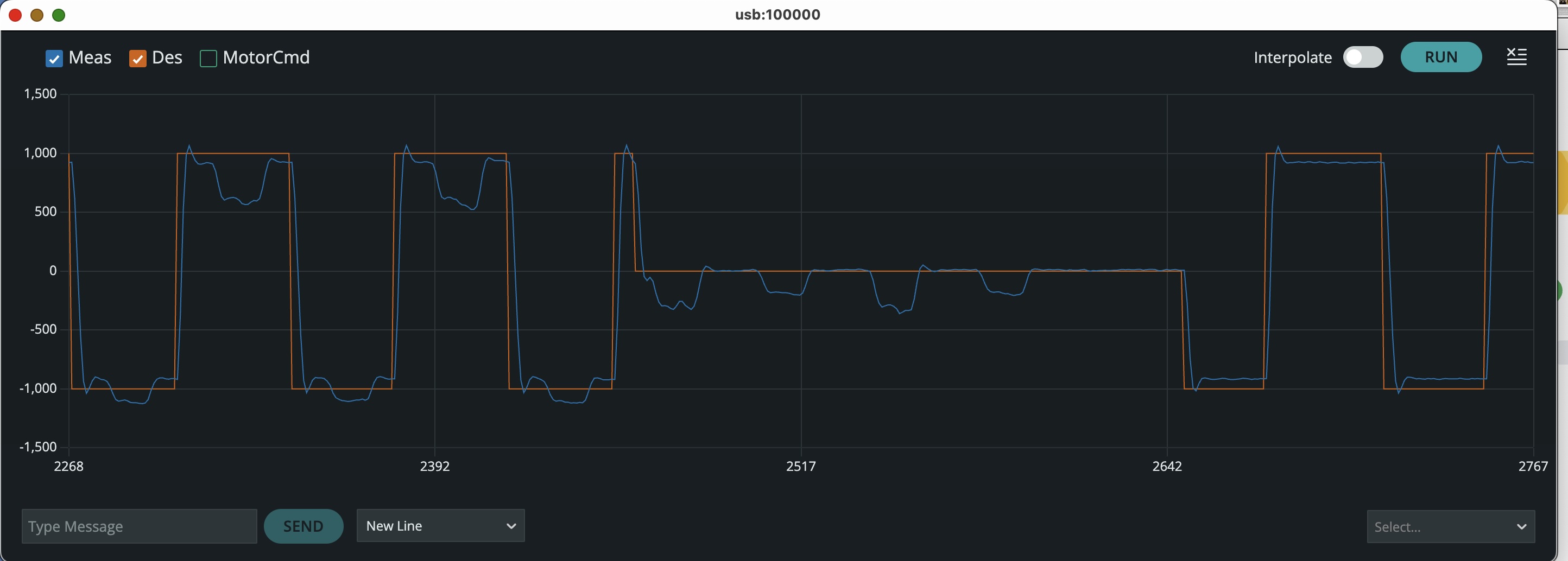
On your system, how does the disturbance response vary with increasing K_p? Try using higher gains by setting ticksperupdate to 4, then 2 and then 1.

Checkoff 4:

  • With the disturbance set to zero, compare the theoretical and measured maximum stable K_p as you vary \Delta T (by adjusting ticksperupdate).

  • What property was our plot above demonstrating?

  • With the input amplitude set to zero, and the disturbance turned on, determine how the disturbance response varies with increasing K_p (adjust ticksperupdate to get higher gains).

  • Repeat the above with the input amplitude set to 1. Does the K_p that minimizes the disturbance response also produce input responses that settle quickly?

Collecting Data for the PostLab.

Today's lab focuses on modeling our speed control system. Generally, the model was reasonably predictive, but perhaps we should look a little closer.

In creating our model, we assumed we could measure the motor speed, but we cannot measure motor speed directly. Instead, we measured the times between ticks that correspond to encoder blades passing under our optical detector. We then estimated speed once per update'' by dividing the amount of rotation of the motor (1 revolution when ticksPerUpdate is 8 or 1/8 revolution when ticksPerUpdate is 1) by the time that elapsed during the update period (one period when ticksPerUpdate is 8 or 1/8 of a period when ticksPerUpdate is 1).

We introduced errors in this estimation process, but we can model those errors and correct for them, as you will explore in PostLab 1. To prepare, you will collect data for different speed estimators (WITHOUT changing Delta T) by adjusting the parameter ticksPerEstimate.

Gather data to analyze in PostLab 1 as follows.

  • Set disturbA on line 14 of the sketch to zero, and reupload the sketch. Then use the send window to set the input amplitude to 1, freq to 0.2, repeats to 3, and adjust K_p so that on the falling transition, the motor speed oscillates three or four times before settling. Take a screenshot of the plot to use for the postlab.

  • Take screenshots of plots from setting ticksPerEstimate equal to 1, 2, 3, 4, 5, 6, and 7. Note ticksPerEstimate has index 7, and should NOT BE CONFUSED WITH ticksPerUpdate, which would change \Delta T. For each case, adjust (AND NOTE) the value of K_p for which, on the falling transition, the motor speed oscillates three or four times before settling. Take screenshots of the plot for each case, to use for the postlab.

There are many subtleties to this experiment, as you will see when you analyze it in the postlab.

Checkoff 5:
  • Show your plots to a staff member, you will analyze them in postlab.