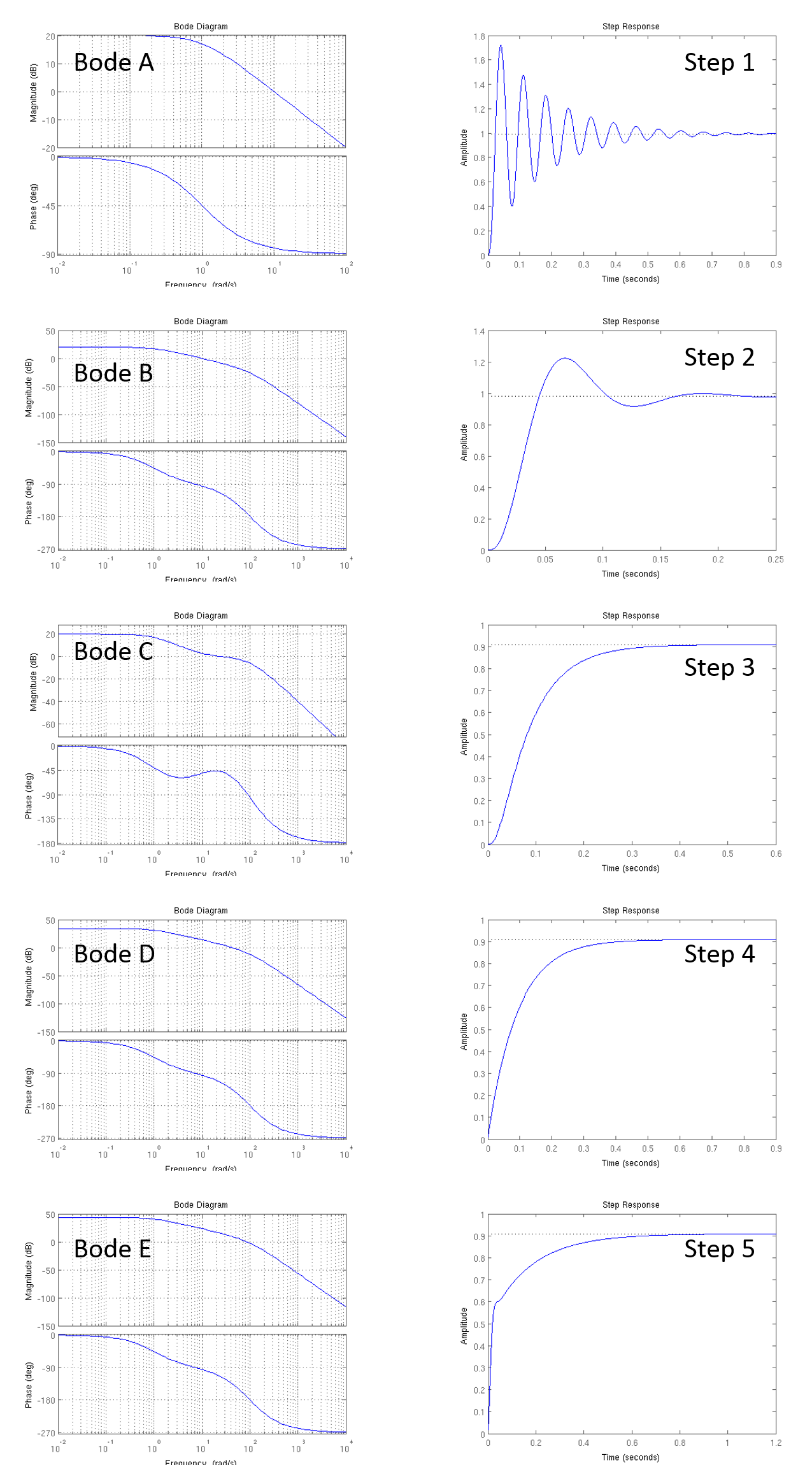
Bode and Steps
Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.
To review the relationship between open-loop frequency response and closed-loop step responses, consider the following Bode plots of open-loop systems, H(s), and the step responses of the closed-loop systems,
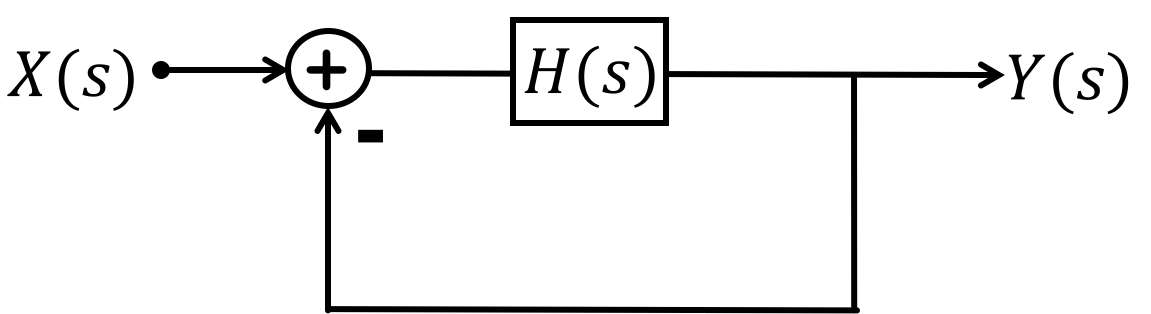
Please match the bode plot of H(s) with the step response of \frac{H(s)}{1+H(s)}. To find matches, you can work backward from the closed-loop system step response. Closed-loop step response features such as overshoot and oscillation period indicate the closed-loop natural frequencies, from which one can infer the closed-loop system frequency response. Given the closed-loop system frequency response, one can estimate the frequency response of the open-loop system. You can also work forward from the open-loop frequency response, with the key being the phase margin of the open-loop system. A small phase margin results in highly oscillatory closed-loop step responses.