Introducing Control Concepts
Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.
Feedback vs. Feedforward
Thermostats, cruise control, camera auto-focusers, scooter stabilizers, aircraft autopilots, audio amplifiers, maglev; all examples that demonstrate the pervasive role of feedback control in engineering design. But not all controllers use feedback. For example, when you stand on one foot, you use feedback control to stay balanced by shifting your weight if you start to fall. But when you kick a ball towards a goal with that same foot, you are using predictive, or feed-forward, control. The ball arrives at the goal because you determined the right way to kick it, not because you corrected its trajectory in midflight (unless the ball is outfitted with a quadcopter, or you are playing a game of quidditch).
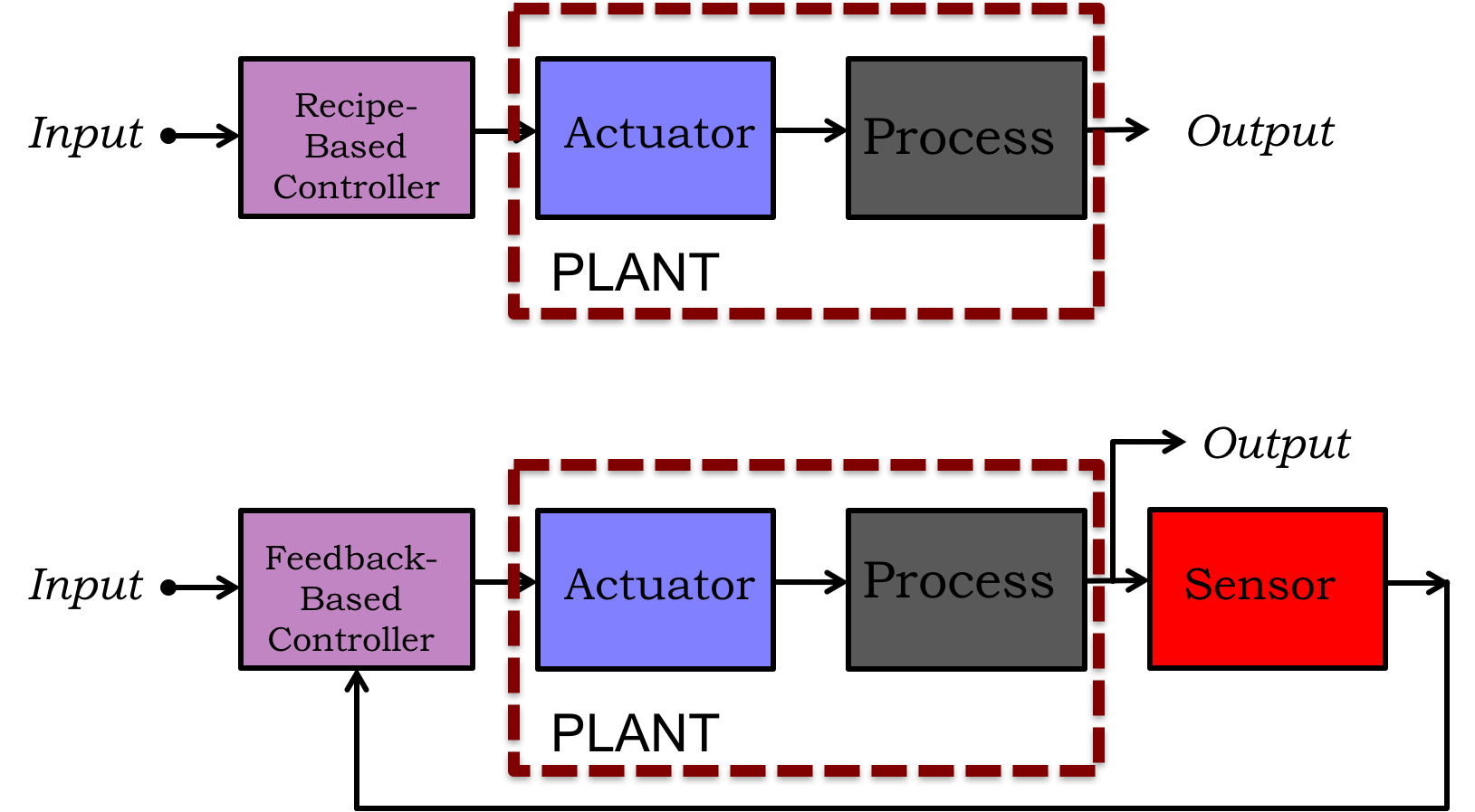
Feedback control has costs and limitations; we will confront some of those in lab this week. In fact, most modern controllers do not rely entirely on feedback, but use combinations of feed-forward and feedback control. But in order to describe those trade-offs, we first need a canonical description of the differences between feedback and feed-foward control. To help you, consider the feedback control (bottom) and feed-forward control (top) block diagrams in the Figure above.
In the figure above, the plant, as indicated by the dashed-line box, refers to the combination of what is being controlled, the process, and an instrument that modifies the process behavior, the actuator. For example, the process could be room temperature, vehicle cruising speed, or camera focus, and the associated actuator could be the furnace in a temperature control system, the car engine in a cruise control system, or the lens-moving motor-and-gears in an camera autofocusing system.
The controller, shown in purple in the block diagram, directs the actuator based on the input. For example, if the input is a desired room temperature, then the controller determines when to start and stop the furnace so that the room stays at the desired temperature. If the controller bases its directions on measurements of the plant state, as in the bottom block diagram, then we say it is a feedback controller, and if the directions are based on a predetermined recipe, we say it is a feed-forward controller.
The sensor block in the feedback control diagram indicates an essential aspect of feedback control, that there is continuous sensing of the state of the plant. In a feedback controller, if the state is perturbed, the controller can easily adapt its directions to correct the state. For example, if one opens a window in a room with a feedback-based temperature controller, the subsequent drop in temperature will be sensed by the controller, and the furnace will turn on to compensate.
You use feedback control when you try to balance on one foot. You continually monitor your "state" (probably how much you are tilting), and weight-shift in the opposite direction to rebalance. In feed-forward control, there is no state monitoring. The controller sends instructions to the actuator by following a recipe. And that recipe is usually based on a model of how the plant will respond. Kicking a ball towards a goal is an example of feed-forward control, because your kick is based on a recipe, and that recipe is based on your mental model of how to get the ball to head towards the goal. Since you can not redirect the ball in mid-flight, you are not using feedback control.
In this course we use a restricted setting so that we can make a clear distinction between feedback and feed-forward control, and so you can learn how to combine them to improve controller performance. But the distinction is not clear in general, and is being further blurred by the introduction of ideas from artificial intelligence and machine learning. For example, reconsider the feed-forward control used in kicking a ball. There is no sensing in the feed-forward block diagram above, yet you have a sensor, you see the ball flying towards or away from the goal. Did you learn a control recipe by kicking a ball many times, observing its trajectory, and making adjustments? If so, you are using feedback, but in a way that goes beyond the notions of feedback and feed-forward control we will use in this class. In lecture, recitation, and labs, you will learn the basic principles for several key concepts in control, but for each concept we cover, there is far more to learn than what we will have time to present in one term.
Hitting the Wall
Suppose you have a simple robot that moves forward continuously when turned on, and remains stationary otherwise. The robot must perform only one task, to move from an initial position, eleven meters from a wall, to a final position, exactly one meter from the wall (see Figure below). Consider two strategies for controlling the robot so it performs this task.
Control Strategy 1: The robot has a timer, and you use it to determine \tau , the interval of time the robot must be turned on to travel ten meters. To have the robot performs its task, your controller (controller 1) first turns the robot on, and then turns it off when the timer reading exceeds \tau seconds.
Control Strategy 2: The wall has a lamp, and the robot has a light sensor. You use them to determine L, the sensor reading that corresponds to one meter from the wall. To have the robot perform its task, your controller (controller 2) first turns the robot on, and then turns it off when the light sensor reading exceeds L.

Question: Which is the feedback controller and which is a feed-forward controller?
Sensitivity to Actuator Variations
We can best understand the differences between the two strategies by considering the impact of changes in the environment or the robot. Suppose the robot's initial position is modified, to twenty-one meters from the wall. But there is no opportunity to run new tests and determine new values for \tau and L .
Question: How would you change the timer-based controller? Do you expect that the robot's final position will still be one meter from the wall?
Question: How would you change the light-sensor-based controller? Do you expect that the robot's final position will still be one meter from the wall?
Consider what will happen if one of the wheels on the robot breaks, and is replaced with larger wheels.
Question:Will controller 1 still position the robot accurately? Will controller 2?
The timer-based controller and the light-sensor-based controller both rely on initial calibration, and both are `making measurements while the robot is moving, but there is a key difference. The timer-based controller is measuring time, and those readings are independent of the robot's distance to the wall. So time measurements cannot be used to correct for changes in robot initial position or changes in wheel size. The light-sensor-based controller's measurements are related to the robot's current position, regardless of how the robot got there. Feeding back these measurements allow the controller to correct for changes in robot initial position or wheel size.
For these two strategies, we see a key attribute of feedback systems, they reduce the impact of variations or disturbances. The light-sensor-based controller always gets us to the right final position, regardless of wheel size or starting position, as long as the sensor is calibrated correctly. We will investigate these ideas more formally below.
Sensitivity to Sensor Variations
There is one more aspect of feedback control that makes it more a tool for an engineer than a scientist. Suppose the light on the wall is replaced by a brighter light. Will controller 2 still position the robot accurately?
No, the robot will end up too far away from the wall. The brighter light will cause the sensor's reading to exceed the L threshold further away than one meter from the wall, and the robot will be turned off. The problem is that the calibration used to relate sensor reading to distance was based on light sensor readings from a dimmer lamp.
For controller 1, we calibrated the actuator by measuring the time to travel ten meters. Of course the controller fails when we change the actuator or the distance to the wall. But the same is true of controller 2. We calibrated the light sensor by measuring the light level one meter from the lamp on wall. Of course controller 2 fails when we switch to a brighter wall lamp.
It is true that by using feedback, we made the robot behavior insensitive to changes in the actuator or the environment, but we also made it much more sensitive to changes in the sensor. So why is feedback so important? The true value of feedback control is that it enables the important engineering trade-off:
It is far easier and cheaper to make an accurate sensor than to make a precise actuator, or to arrange for a consistent environment.The Propeller Speed Control Lab
Throughout this class, we will try to weave together three concepts: strategies for constructing mathematical models for systems of interest, techniques for characterizing that model's behavior, and approaches to feedback control based on insights from the modeling and characterization.
In this first lab, we will focus on first-order systems, and will investigate controlling them using proportional feedback and feed-forward control. We will start by modeling first-order systems using difference equations, and learn how to characterize the model's behavior using natural frequencies. In lab, you will use these ideas to design discrete-time feedback/feed-forward approaches that control the speed of your copter's propeller by sensing the motor speed and then adjusting the motor current.