Lead Compensation
Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.
What follows is a very brief discussion of lead compensators, with some short questions interspersed. We are trying to convey a sense of "why is this useful" and the "how to design with it", and not focus on formal guarantees. In a few weeks, we will switch to state-space, a better setting in which to be formal.
We have usually divided the forward path of our archetype feedback system in to the controller (what we design), with transfer function K(s) , and the "plant" (what we are controlling), with transfer function H(s). We will deviate slightly from the K(s) and H(s) notation, and further divide the controller in to the product of a constant gain K_0, and a normalized compensator transfer function, H_c(s). In this way, candidate compensators can be more easily compared. A good compensator is not the one with the highest innate gain, but the one that, after optimizing over K_0, yields a feedback system with the smallest tracking errors and highest disturbance rejection.
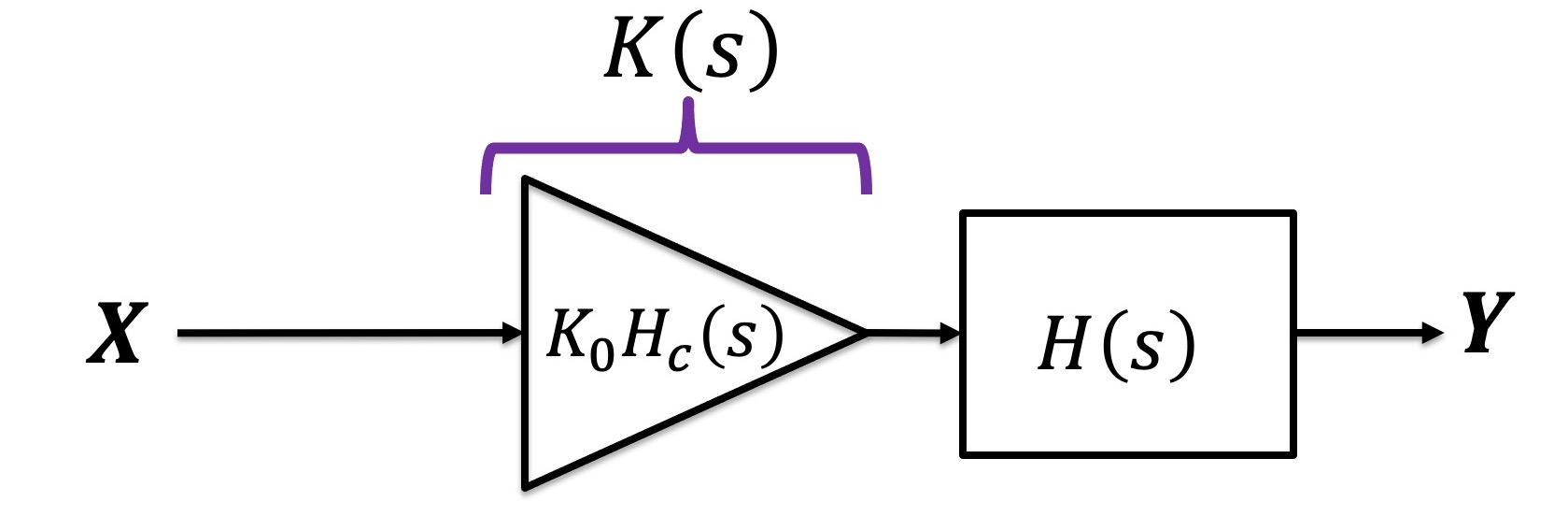
Then suppose we "close the loop" around the system, as below
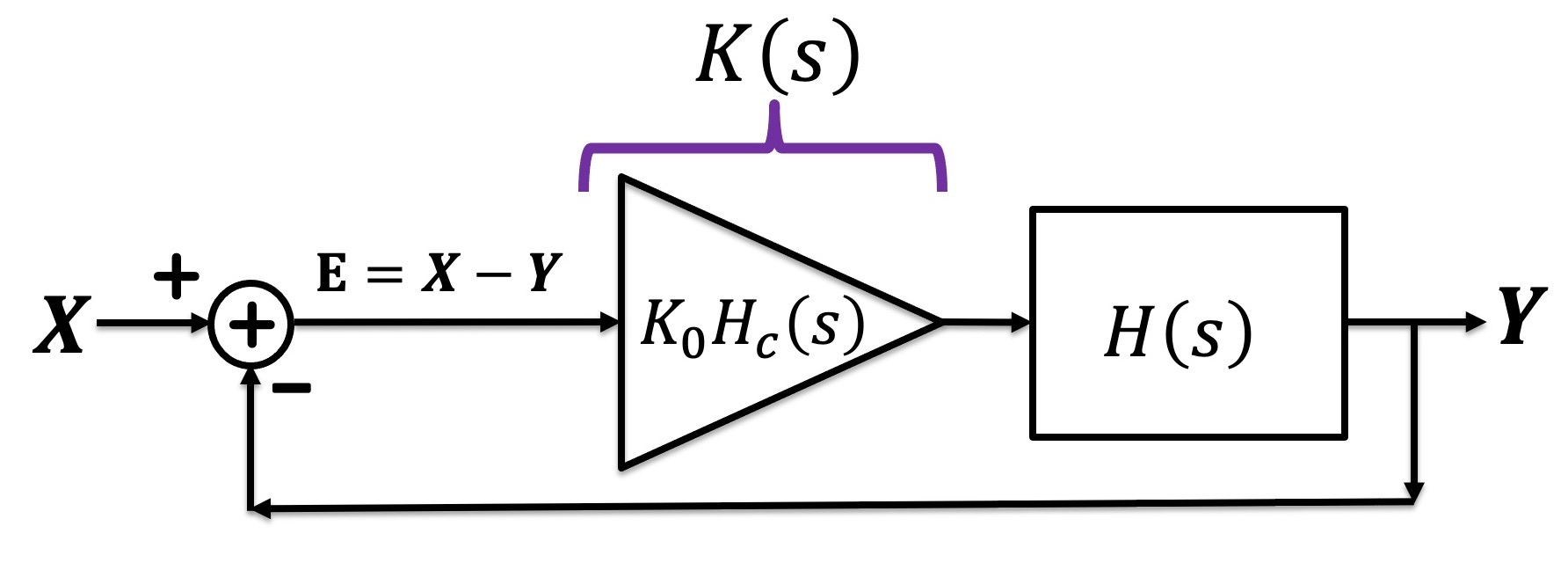
where we can use what should be the comfortably-familiar Black's formula to derive
When we are referring to the closed-loop transfer function, we will denote it as G(s), where G(s) is given
If x(t) = e^{j\omega t} for all -\infty \le t \le \infty (a mathematical idealization), then in closed-loop,
If a system is stable, we can measure the frequency response by applying unit amplitude sinusoidals, waiting until the output achieves sinusoidal steady state, and measuring the amplitude and phase shift of the output. Even if a system is not stable, the above construction can be evaluated mathematically, but not measured practically.
What happens if the denominator in the expression for the closed-loop frequency response,
In fact, K_0 H_c(j \omega_0 ) H(j \omega_0) need only be close to -1 to cause problems, and the closer it is to -1, the further G(j\omega_0) will be from unity. One can make a more formal link to closed-loop stability, but for now, it is sufficient to note that IT IS BAD FOR
For K_0 H_c(j \omega_0 ) H(j \omega_0) to equal -1, an angle and a magnitude condition must each be satisfied:
-
Magnitude condition: |K_0 H_c(j \omega_0 ) H(j \omega_0)| must be equal to 1.
-
Angle Condition: \angle \left( K_0 H_c(j \omega_0 ) H(j \omega_0) \right) must equal +\pi or - \pi radians or +180 or - 180 degrees.
Since being exactly equal to -1 is unlikely, but being near is also bad, we need to define metrics for how close we are to the dreaded -1. To that end, there are three terms commonly used to describe the closeness:
-
Unity gain frequency ( \omega_{unity}): the value of \omega such that |K_0 H_c(j \omega_{unity} ) H(j \omega_{unity})| = 1 . It is possible to have multiple unity gain frequencies, though it is uncommon.
-
Phase Margin : How far the \angle \left(K_0 H_c(j \omega_{unity} ) H(j \omega_{unity})\right) is from - \pi or +\pi radians or +180 or - 180 degrees when the magnitude is unity. Phase margin is usually specified in degrees, and is (in degrees):
- Gain Margin : For those values of \omega for which
\angle \left(K_0 H_c(j \omega ) H(j \omega)\right) equals either
+180 or - 180, the gain margin (in dB) is defined as
-1 times the least positive 20 \log |(K_0 H_c(j \omega ) H(j \omega))|.
If the gain margin is negative, then
|(K_0 H_c(j \omega ) H(j \omega))| > 1for all \omega's for which the phase is 180 degrees.
Phase and gain margins can be positive or negative, but they are only guaranteed to indicate a problem when they are close to zero. To better understand what we mean by "problem", consider the three-pole example in the next section.
Consider the three-pole example
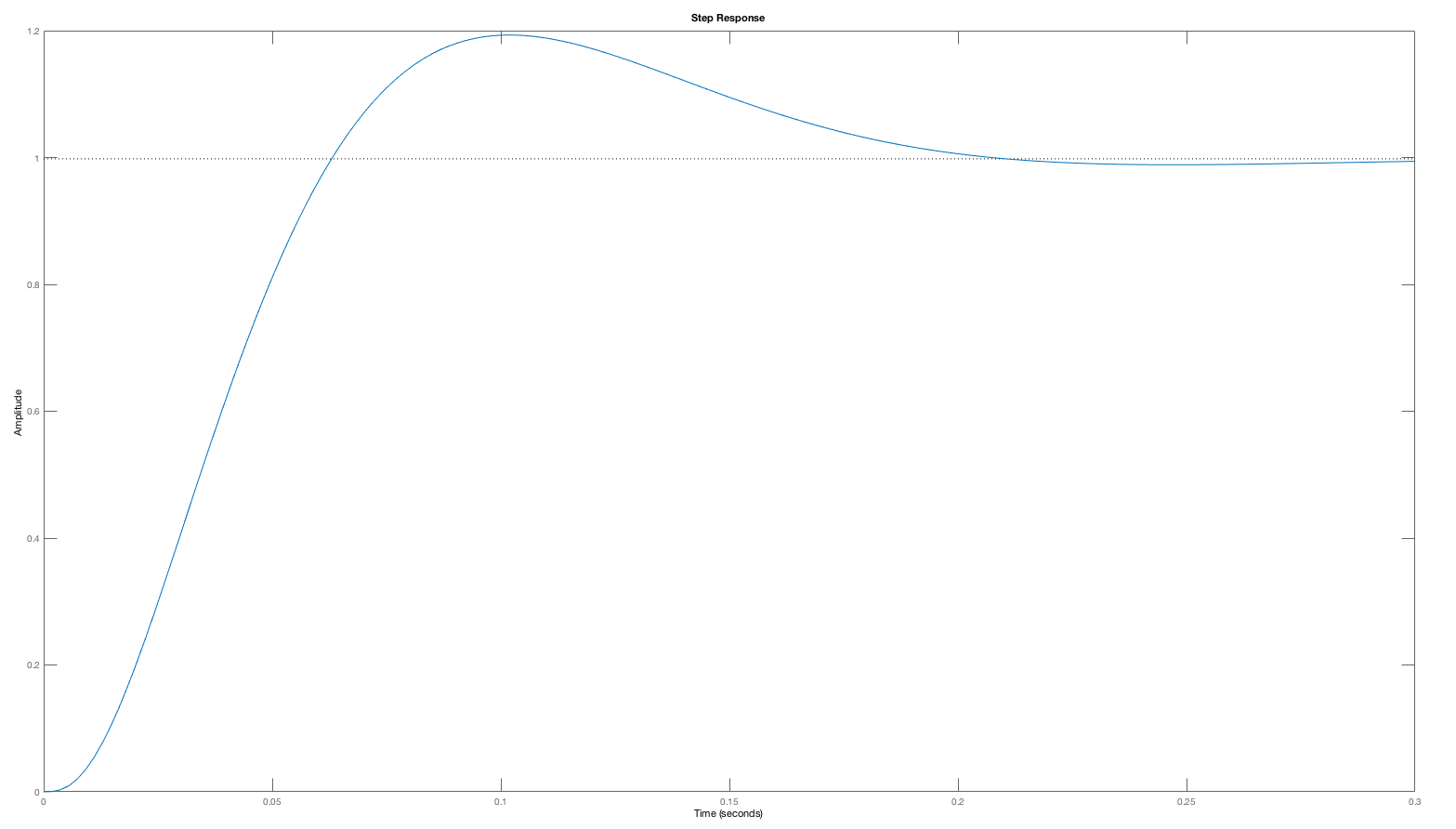
Consider the open-loop margin plot and the closed-loop step response for the cases K_0 = 5, 20, \; and \; 50 below. As is clear from the plots, the phase margin decreases with higher and higher gains (values of K_0), and the step response becomes more oscillatory. The low phase margin was a correct indication of a problem, as the oscillation in the step response at K_0=50 is certainly a problem.
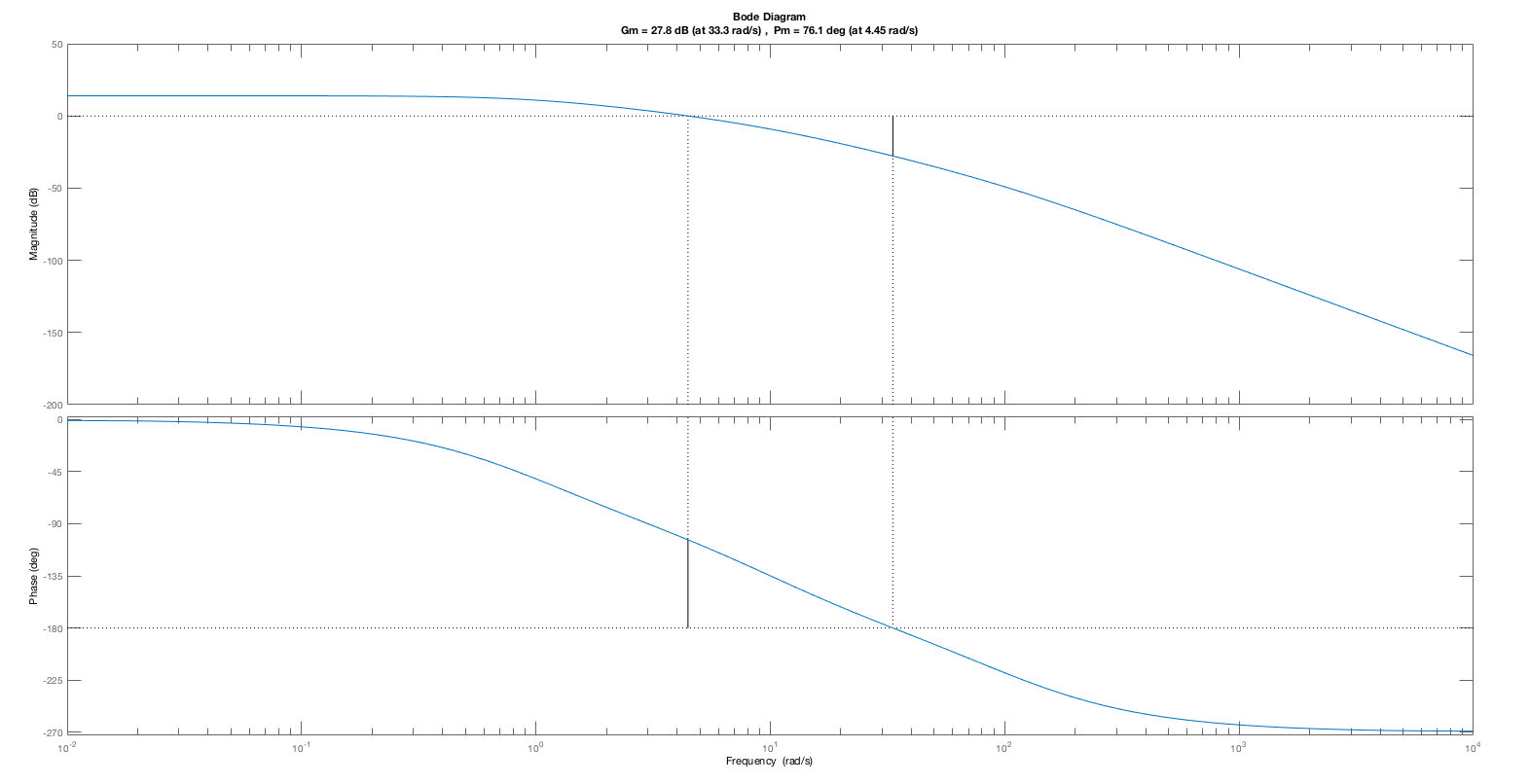
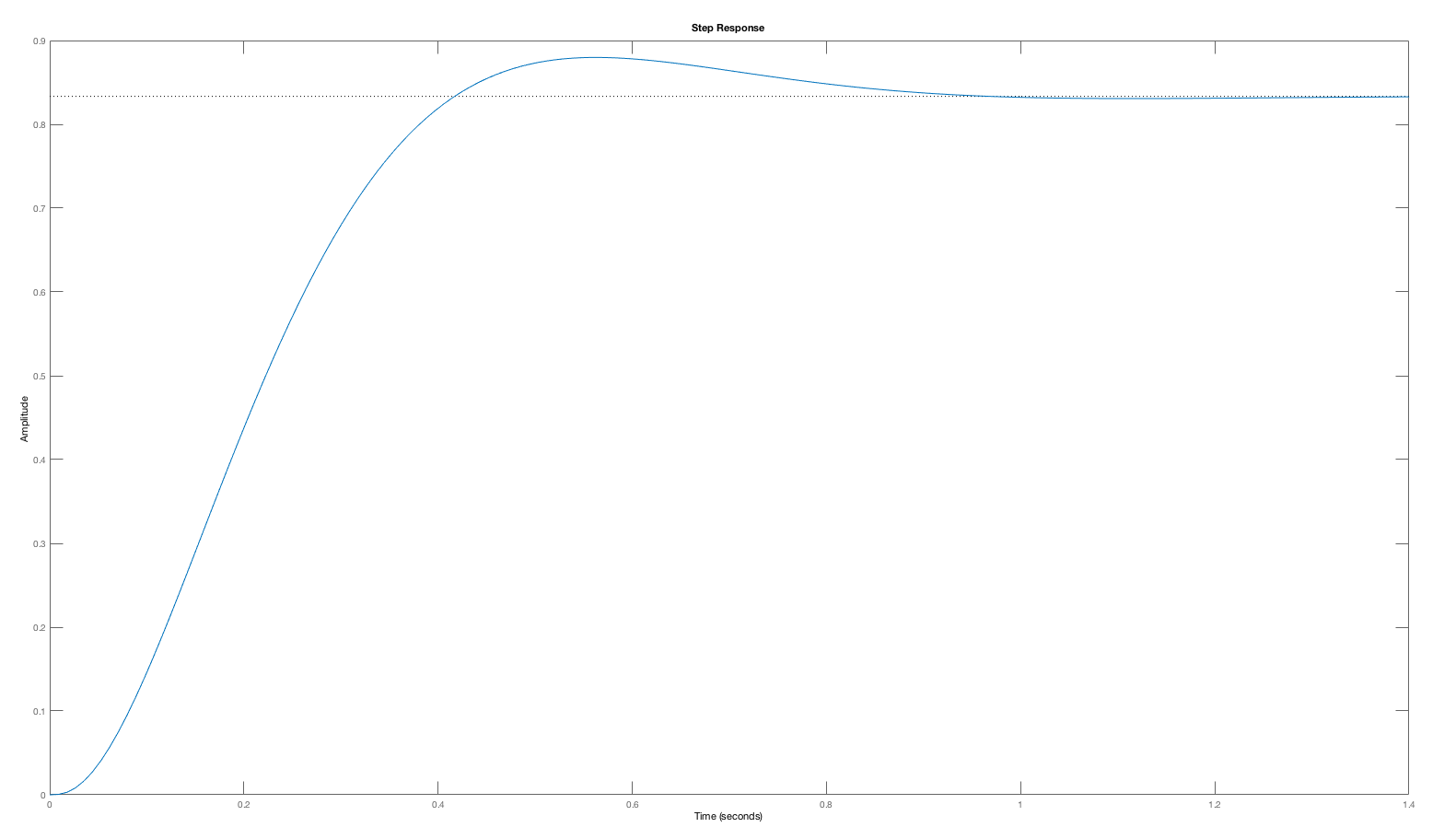
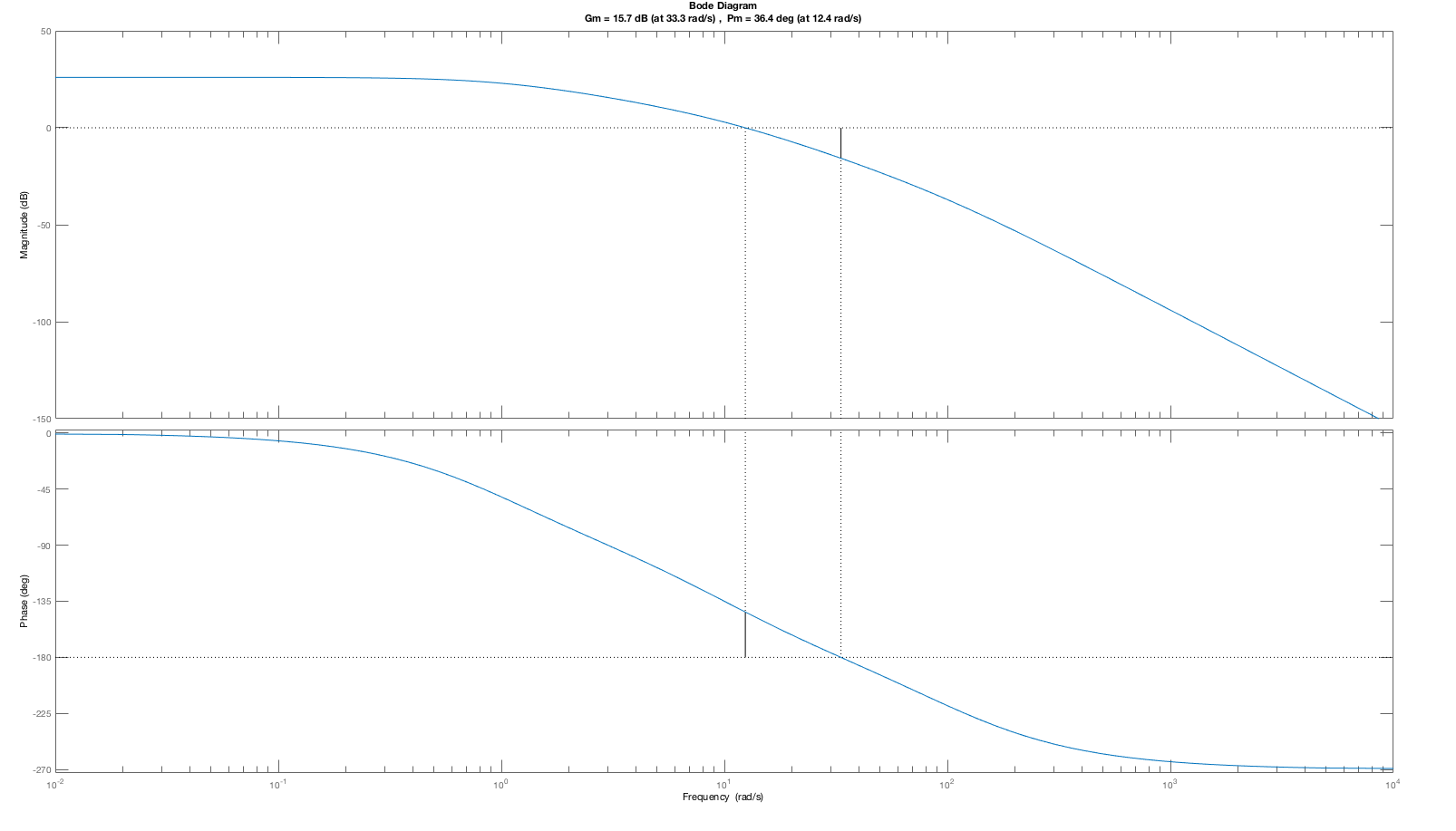
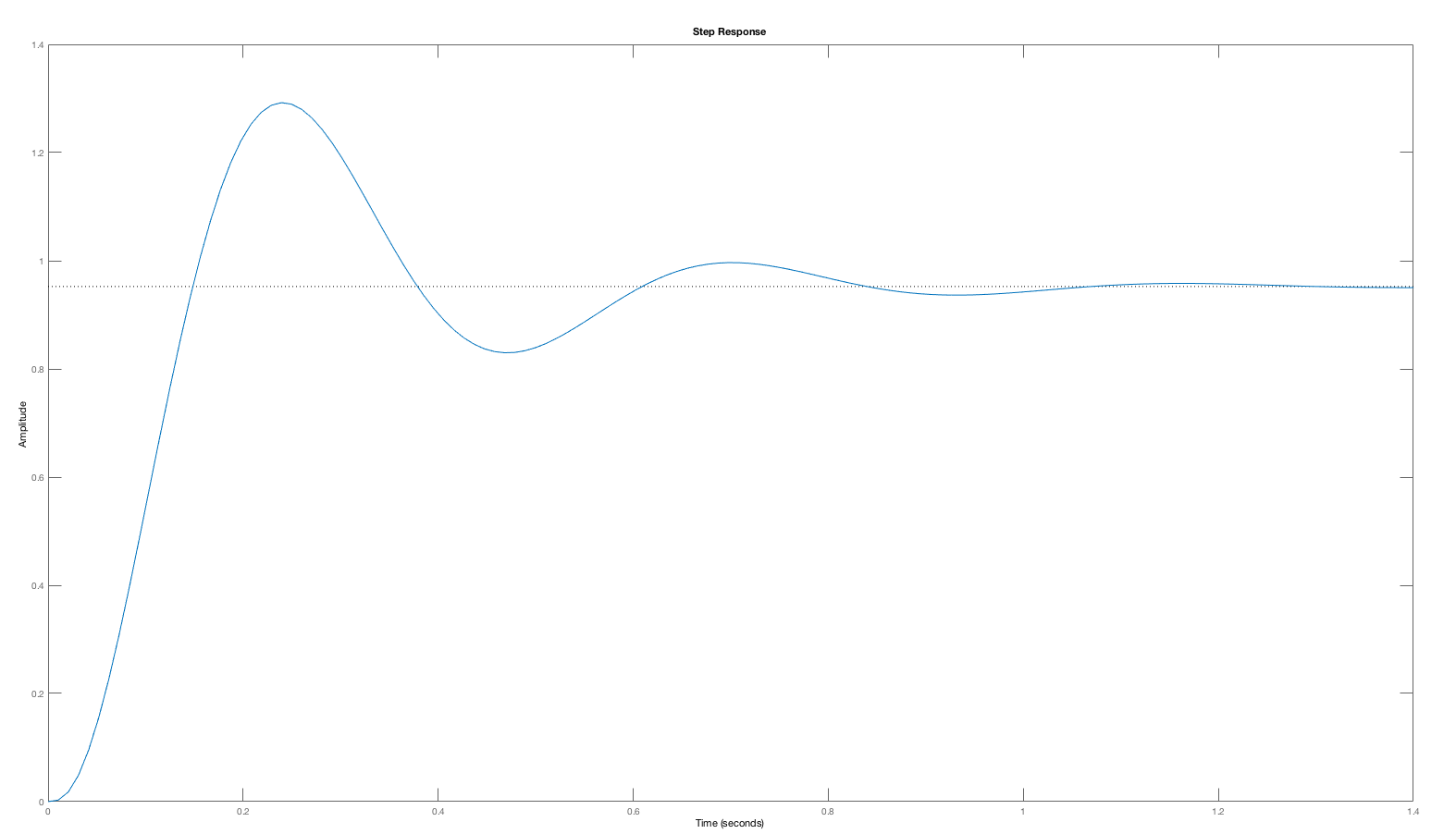
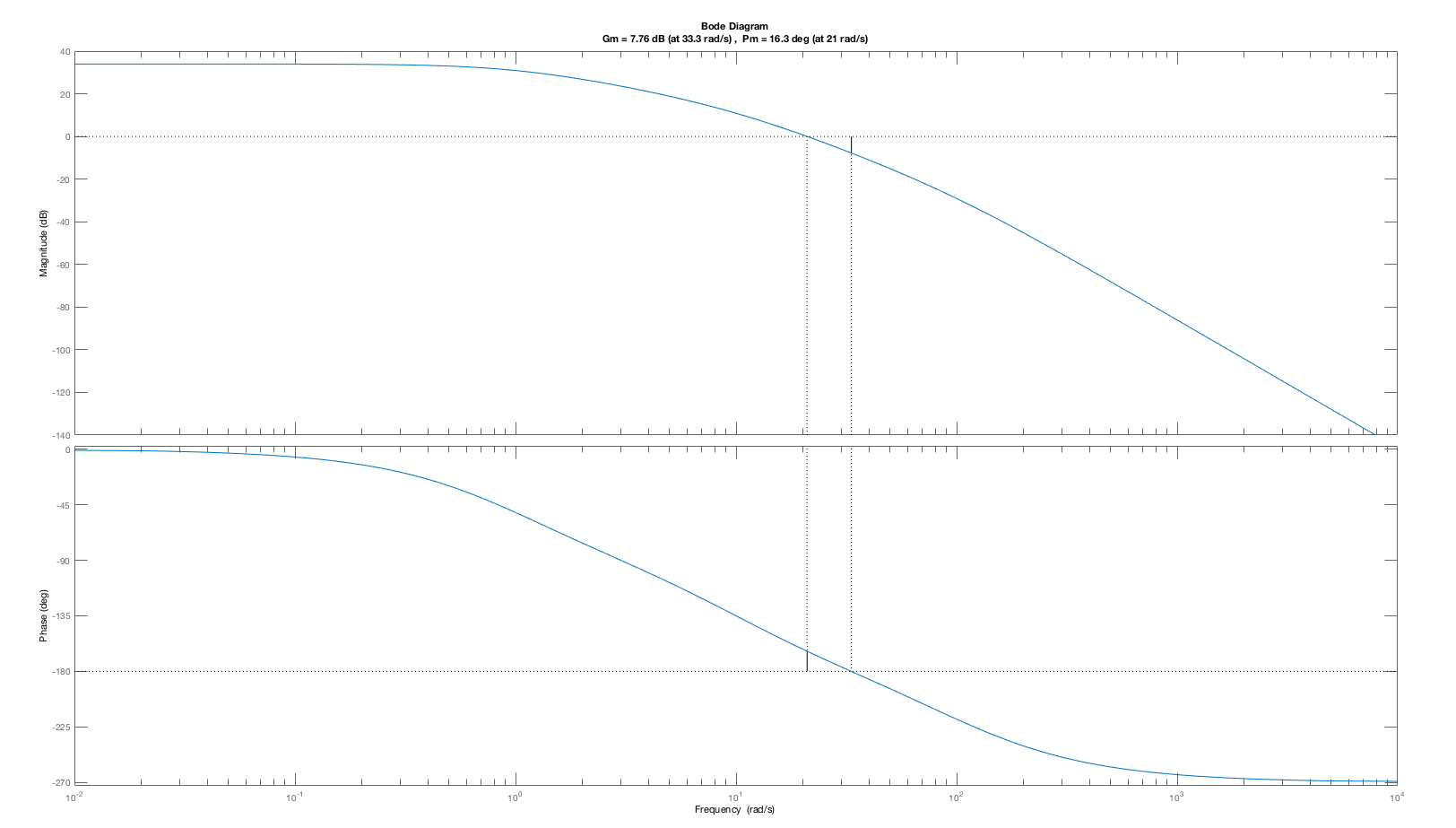
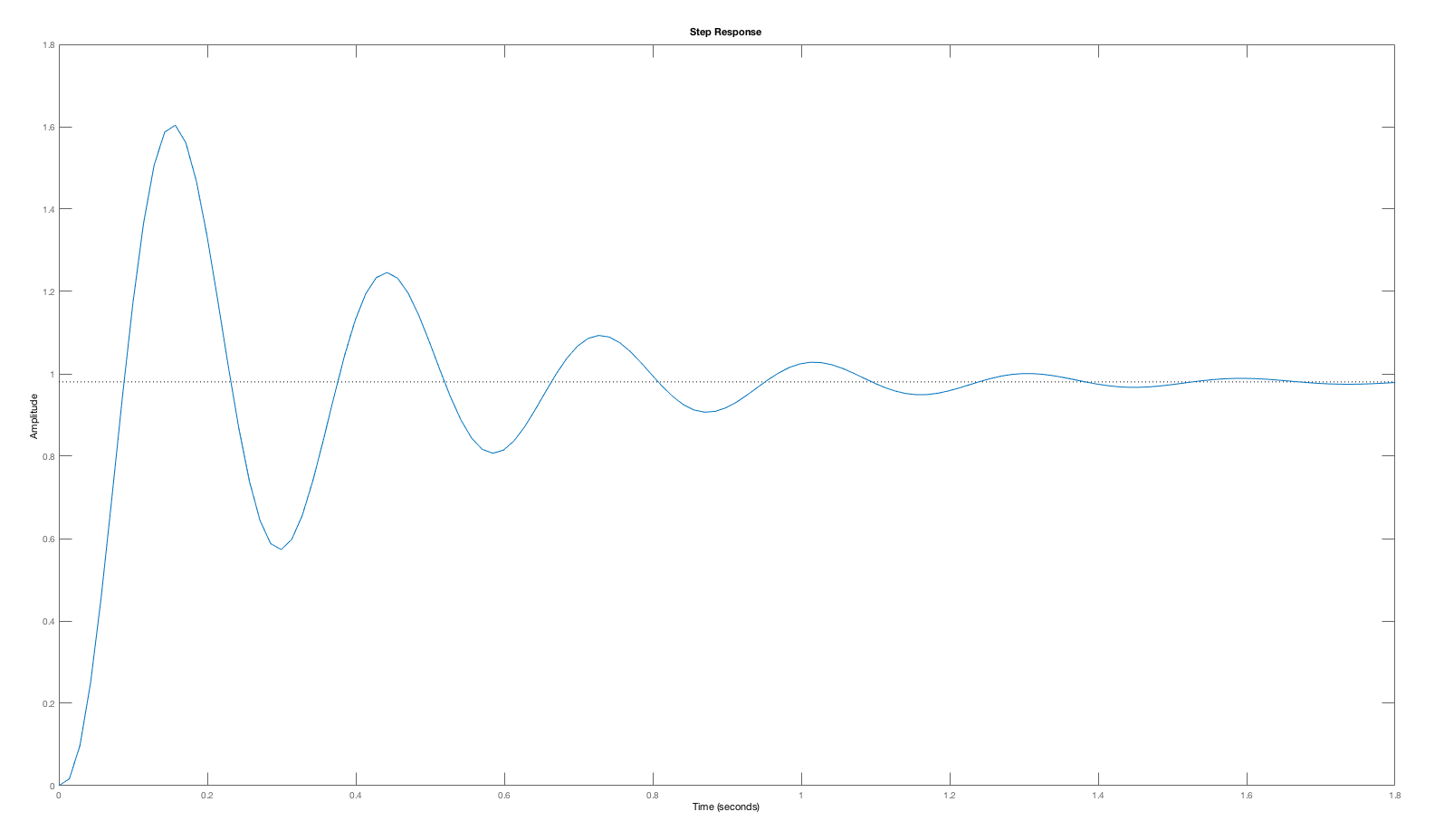
One might expect that an open-loop system with a small phase margin will likely result in a closed-loop system with an oscillatory step response, such as the particularly pronounced K_0 = 50 case. But phase- margin-based predictions are not quantitative. The oscillation amplitude of a closed-loop system, including its oscillation frequency, is far more readily predicted by considering the Bode plot for the closed-loop system with K_0=50 (see figure below). As the Bode plot for the closed loop system shows, the frequency response has a large peak, exactly at the frequency of the oscillating step response. Or, we could have considered the root-locus plot for this system, which would have indicated that at K_0=50, the poles of the closed-loop system move close to the imaginary axis (the second figure below). Finally, when K_0=5, the gain is too low to accurately track the input, and the steady state value for the step response (which should be one) is off by more than ten percent. Phase and gain margin tell us little about this low gain problem.
So, why bother with gain and phase margin?
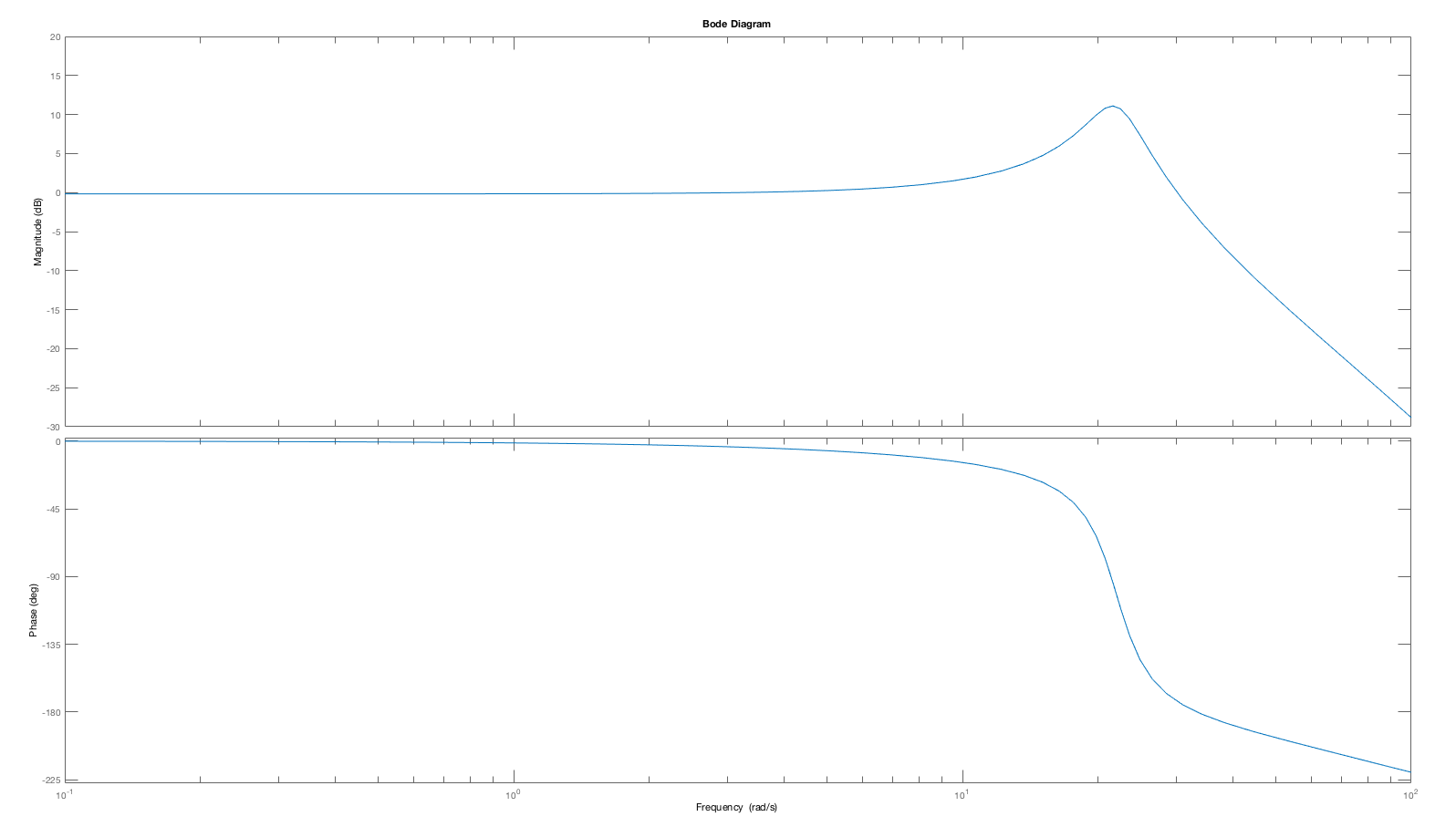
Bode Plot of the CLOSED-LOOP response for the K_0=50 case, showing
the peaking of the response at \approx 22 radians/second.
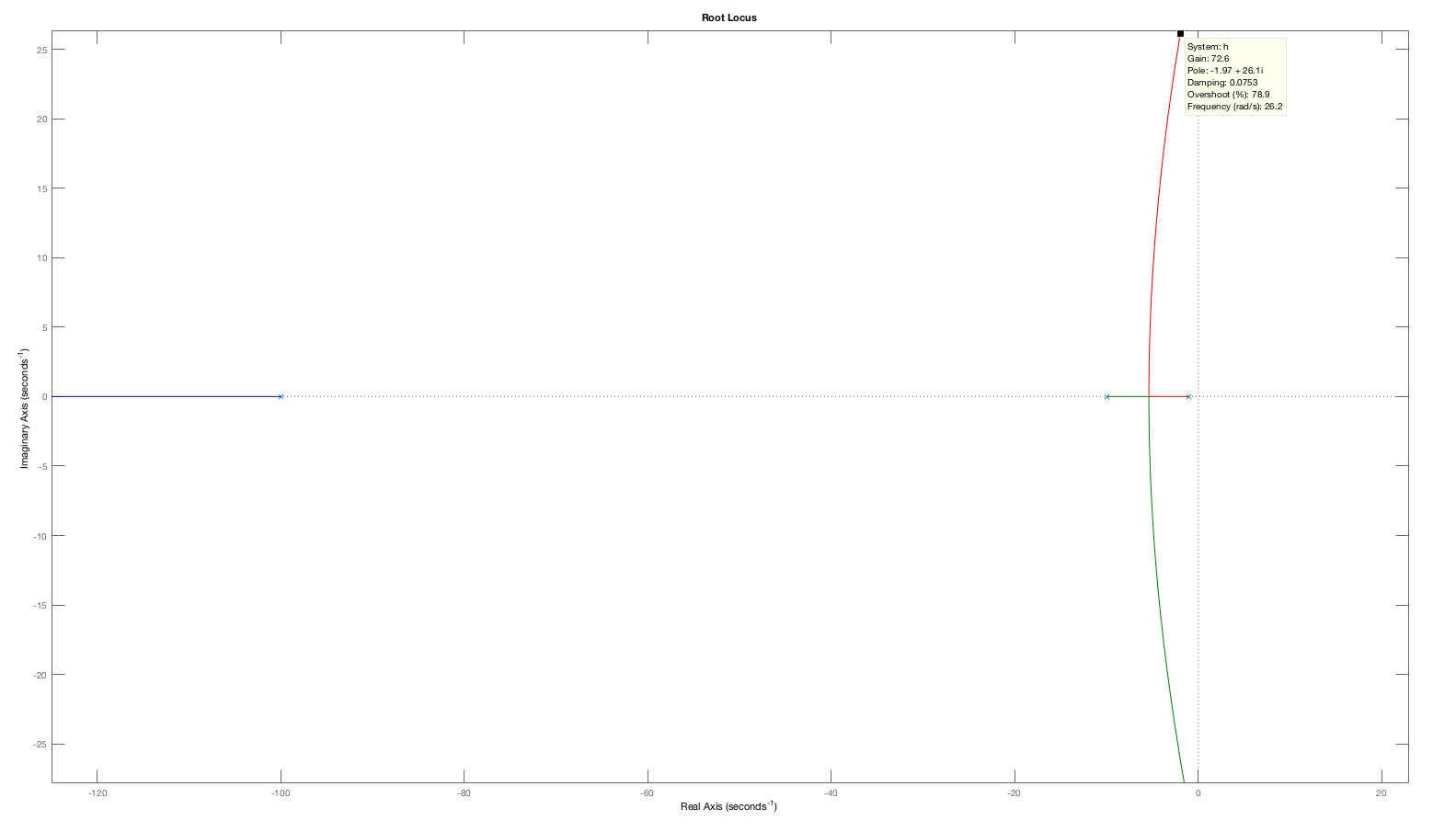
The root-locus plot for H(s) = \frac{1000}{(s+1)(s+10)(s+100)} ,
showing a pair of poles moving towards the imaginary axis as the
gain increases (the highest gain shown is K_0 \approx 70 ).
We know that a small phase margin is bad, but as noted above, we have other tools that can provide a far more sophisticated analysis of the kinds of problems indicated by a low phase margin. On the other hand, if we do have low phase margin, there is an easy way to design a compensator to increase it.
The key insight to increasing phase margin is that the angle for a product of two transfers functions is the sum of the two angles. That is,
To see how to use this additive property, suppose K_0 H(s) has a small phase margin. For systems dominated by poles (as most physical systems are), the angle of the frequency response will be negative. Then since the phase margin is small, the angle at unity gain must be close to -\pi, or in degrees,
But not so fast! We can not exactly enforce the unit magnitude constraint, while still adding phase, but we can come close. And, we can come close with a transfer function that is easily implemented (in continuous time with a circuit, or approximately in discrete-time, as we shall set later).
Consider a normalized compensator transfer function:
What is magnitude of the normalized compensator at zero frequency?
In terms of s_p and s_z, what is the magnitude of the compensator in the limit as \omega \rightarrow \infty? Use s_p to denote s_p and s_z to denote s_z,
Can we use this zero-over-pole compensator to add phase at the unity gain frequency? And can we come close to keeping the magnitude of the compensator near one, so we do not shift the unity gain frequency?
Consider the example of a compensator whose zero is s_z = -10, and whose pole is s_p = -100. With this pole and zero, the resulting compensator is of the form
In the figure below, there are three plots. One is a plot of H_c(s), whose magnitude is level, and then monotonically increases, before leveling off a factor of ten higher. Its angle increases, but visually, it seems to start increasing at a lower frequency than its magnitude increases. Perhaps we can use this to approximate our ideal phase margin increaser.
Overall, the angle of the compensator rises from an angle of 0, achieves a maximum, and then returns to an angle of 0. We also show the seperate components in the plot below. There is the angle and magnitude for just the numerator zero, which is flat until the zero frequency and then the angle and magnitude increase monotonically. There is also the angle and magnitude for the denominator pole, which is also flat until the pole frequency, and then starts monotonically decreasing in angle and magnitude.
NOTE: we refer to this compensator as a LEAD compensator because the zero leads the pole.
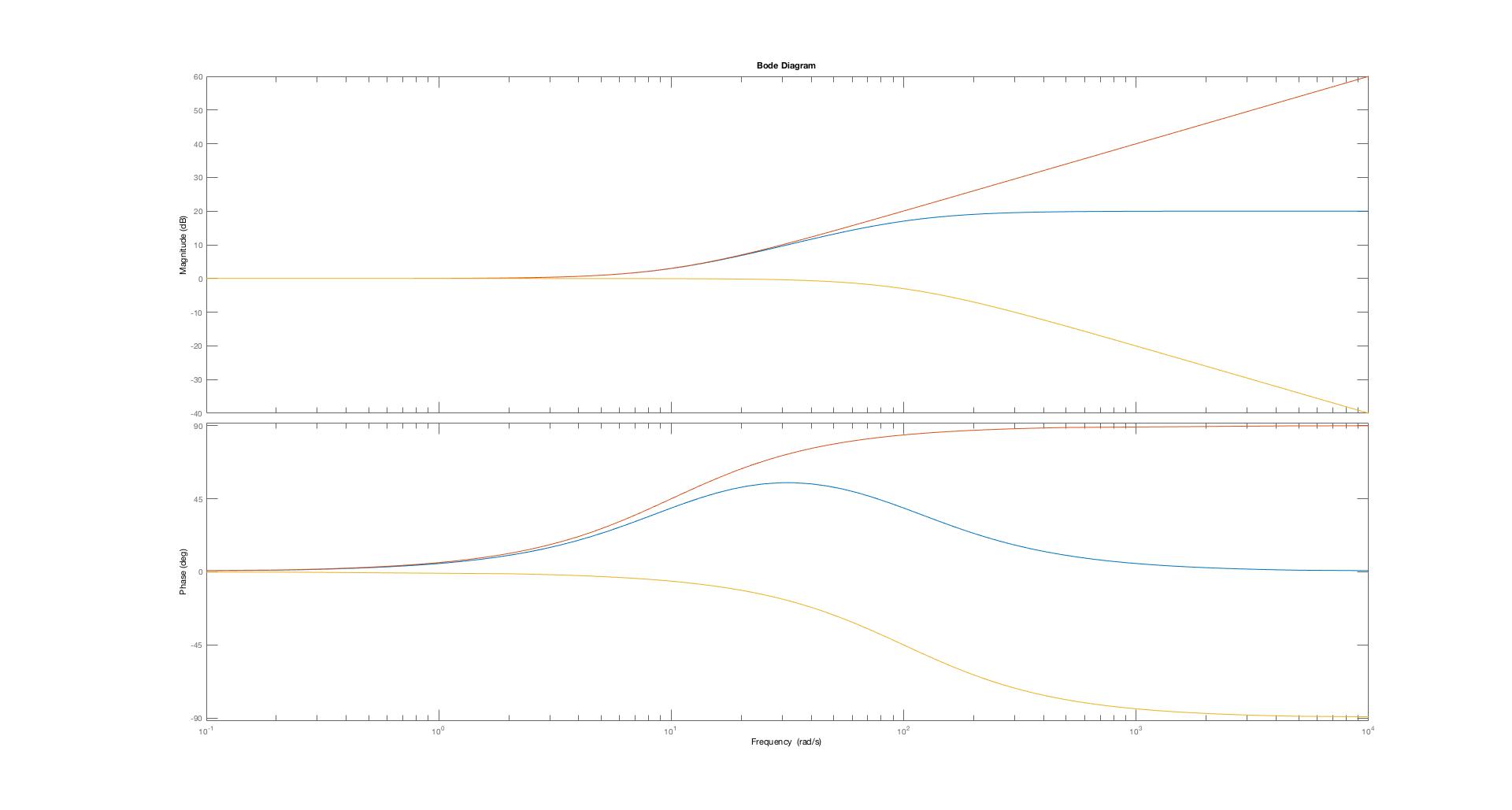
Suppose H_c(s) = \frac{s_p}{s_z} \left(\frac{s-s_z}{s-s_p} \right) , with real s_z, s_p < 0. In terms of s_p and s_z, what is the value of \omega_{extreme} , the frequency where the angle of H_c(j \omega ) achieves its extreme (either maximum or minimum)? Hint: recall that the angle of H_c is the angle of the zero minus the angle of the pole. So differentiate the difference with respect to \omega , and find where the derivative is zero. Use s_p to denote s_p and s_z to denote s_z.
Let us return to the worst example from above, H(s) = \frac{1000}{(s+1)(s+10)(s+100)} with K_0 = 50. The phase margin is quite low, roughly 15 degrees, and the step response oscillates. Suppose we place a normalized compensator with a zero at approximately the unity gain frequency ( s_z = -20 ) and a pole at a ten times higher frequency (s_p = -200)? What is the new phase margin (you will need a bode plotter, use either matlab or python). To check yourself, we have plotted the step response of the compensated system (which is QUITE an improvement).