Frequency-Response-Based Controller Design
Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.
This is a long prelab, intended to prepare you for the maglev design problem next week. It also introduces you to the matlab suite of computational tools for system analysis, tools which we will be using extensively for the remainder of the semester. We had intended to switch over to python exclusively this term, but that transition will have to wait until next term. We've had less time for development than expected, and we did not realize the diversity of python enviroments we would need to support. Our apologies for this, and we will try to make this change in plans as painless as possible.
You can use matlab on-line or install it on your computer, information on the alternatives for MIT students is available here. If you are new to matlab, we suggest using the on-line version, and there is a tutorial video here, but we will describe most of the commands you will need.
For this Friday's lab, if would help to skim over the matlab tools for creating CT transfer functions and computing step responses. But before beginning the design problem next week, you should finish this prelab.
In much of the literature on linear systems analysis, the term "frequency domain analysis" is a very general catagory, and encompasses nearly every use of transforms to replace difference or differential equations involving functions of n or t, with rational functions (typically) of z or s. But when WE use the term "frequency response", we are referring to a system's eventual response to sinusoidal inputs as a function of the sinusoid frequency (the sinusoidal steady-state response). And we usually characterize the frequency response by its magnitude and angle (or phase) with respect to the input sinusoid.
When one uses
It is tempting to try to formalize these easily understood frequency response plots, and focus on connecting plot properties to guarantees about system performance. We will take an alternative approach, and instead focus on using frequency response as a tool for suggesting design alternatives. In particular, we will examine the notion of
Design is different from analysis, and is often more about generating worthwhile alternatives than providing a-priori guarantees. Assuming, of course, that one has the tools to verify any final design.
You can use matlab to manipulate continuous-time transfer functions. First, you have to tell matlab to use s as the CT transform variable, by typing
>> s = tf('s')
After that, you can define a CT transfer function. For example, suppose your system is described by a set of differential equations
In matlab, if you type
>> H = (1/(s+0.1))*(1/s)*(1/s)
Matlab will response with
H =
1
-------------
s^3 + 0.1 s^2
Then if you type
>> pole(H)
matlab will respond with poles (or natural frequencies),
ans =
0
0
-0.1000
as you would expect since in CT, two of your poles are at zero.
We will make extensive use of the step, feedback, and bode commands. You can find information about any matlab command by typing, for example,
help step
to find out a little about the step command, or
doc step
to launch a documentation page with comprehensive information.
If you wanted a Bode plot of H(j \omega ) based on the H described above, you could type
bode(H)
As a more complete example, consider a system with input x(t) and output y(t) described by a first-order differential equation,
In this case, the system function is H(s) = \frac{1000}{s+1}. We say x(t) is equation to a unit step if x(t)=0 for t < 0, and x(t) = 1 for t \ge 0. To plot the response to the unit step using matlab, in the command window type (be sure you have defined s to matlab using s = tf('s')).
H = 1000/(s+1)
to define the system function to matlab, and then
step(H)
to plot y(t) given x(t) is a unit step. Note that y(t) rises to 1000 with a time constant of one second (about two-thirds of the rise in one second).
The frequency response of this first-order system can be plotted using
bode(H)
A Bode plot which labels the unity-gain (|H(j\omega)|=1) frequency, and its associated phase margin, can be plotted using
margin(H)
If we use feedback with this first order system, so that
G = feedback(1000/(s+1),1)
In order to plot the locus of poles of G(s) as a function of K_0 of
rlocus(1000/(s+1))
Root locus plots can be used to select a good controller. For example, for third-order system given by
rlocus((s+4)/((s+20)*(s*s+2*s+1)))
hold on
rlocus((s+8)/((s+20)*(s*s+2*s+1)))
rlocus((s+12)/((s+20)*(s*s+2*s+1)))
rlocus((s+16)/((s+20)*(s*s+2*s+1)))
The above commands will generate a plot like the following (where we have recolored the lines and added a legend). Note that the controllers zeros at -4,-8,-12, and -16 generate root loci that have progressively less negative real parts, for worsening stability.
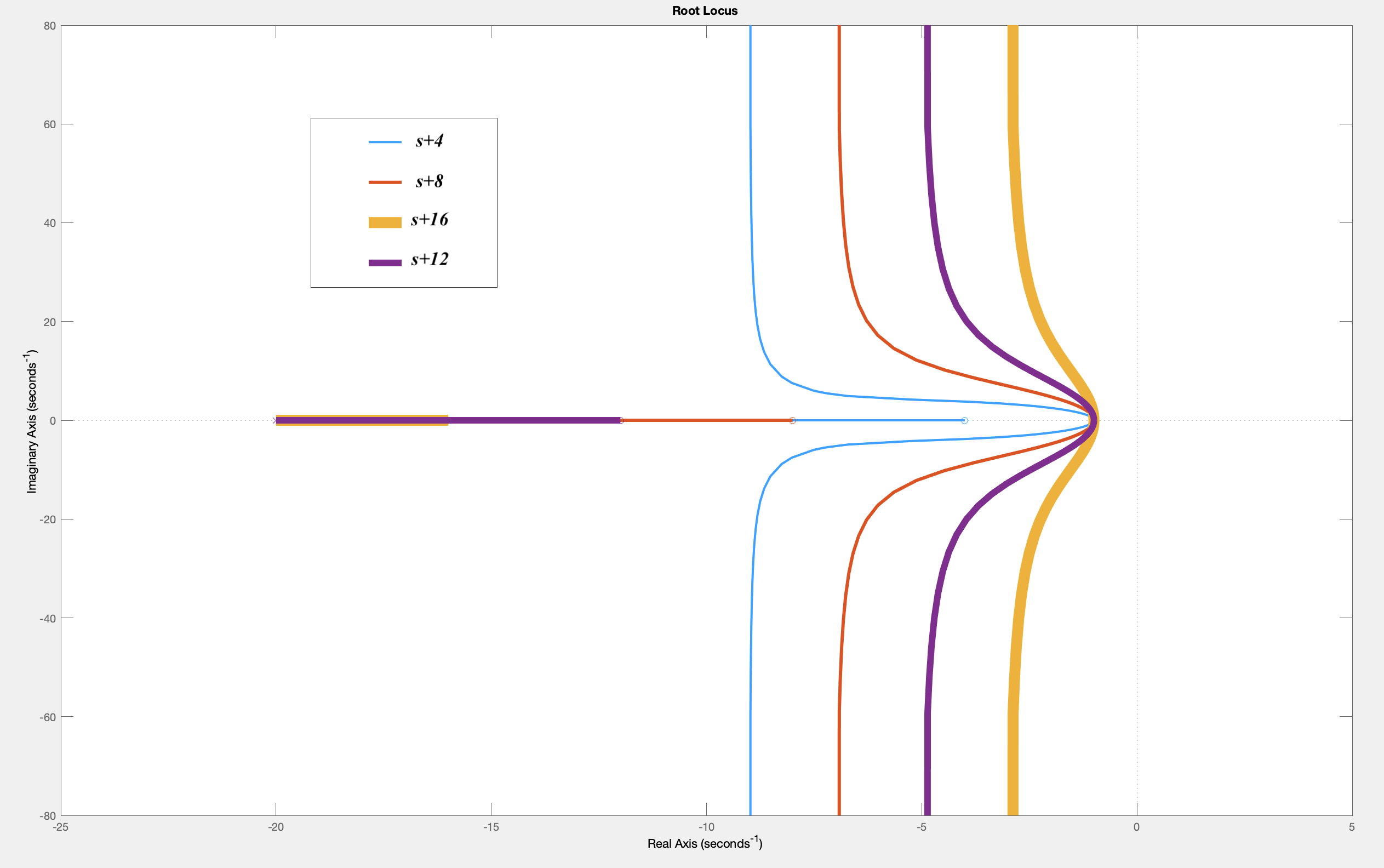
To plot the step response of the feedback system,
step(G)
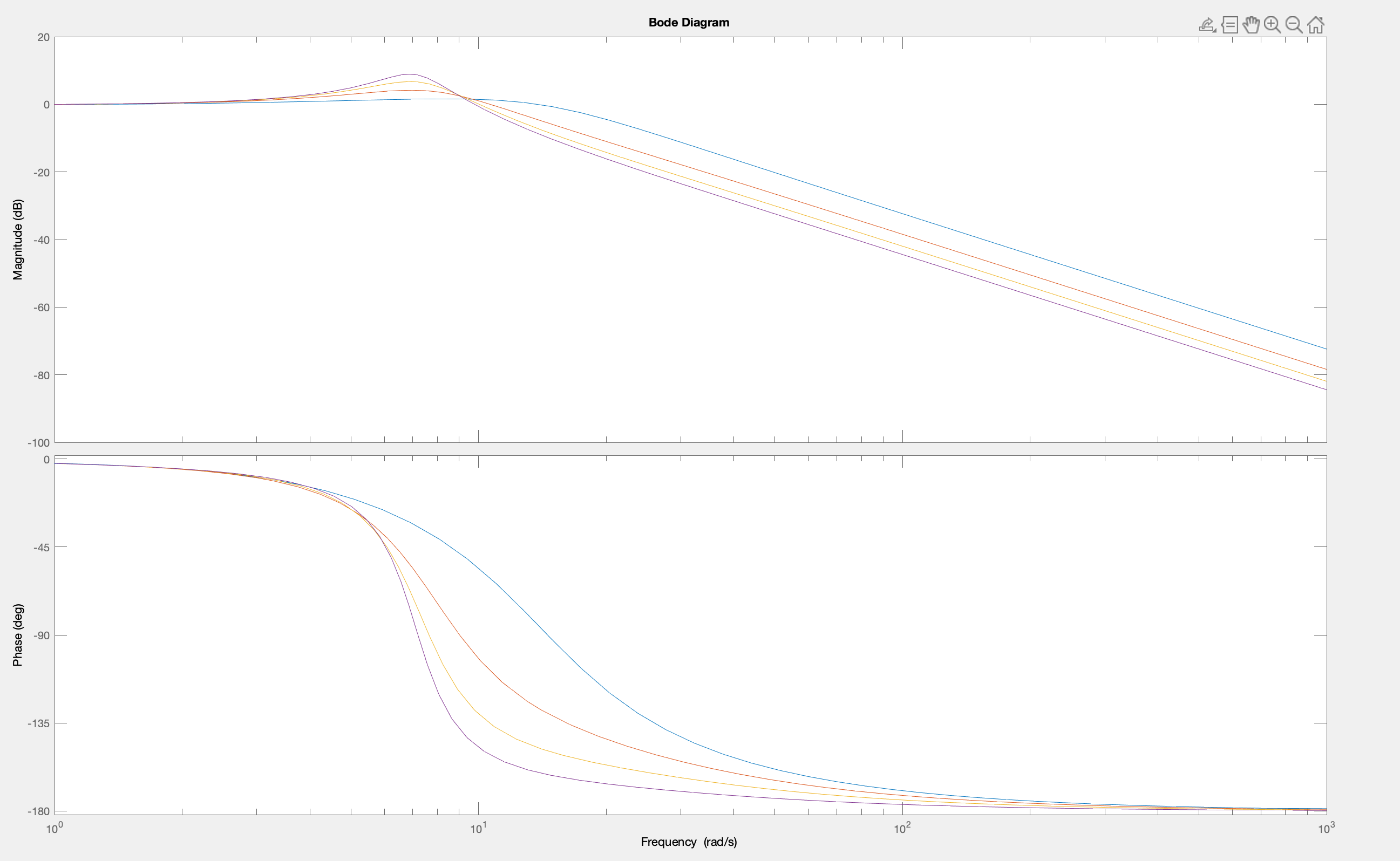
The frequency response also shows the impact of including the first-order system in a closed loop, as can be seen in the plot generated by
bode(G)
For our third-order example, the step responses for the closed-loop systems can be compared, where notice that we have set a scale factor for each controller so that they all have the same steady-state value, K(j\omega)H(j\omega) for \omega = 0.
step(feedback((240*(s+4)/((s+20)*(s*s+2*s+1))),1))
hold on
step(feedback((120*(s+8)/((s+20)*(s*s+2*s+1))),1))
step(feedback((80*(s+12)/((s+20)*(s*s+2*s+1))),1))
step(feedback((60*(s+16)/((s+20)*(s*s+2*s+1))),1))
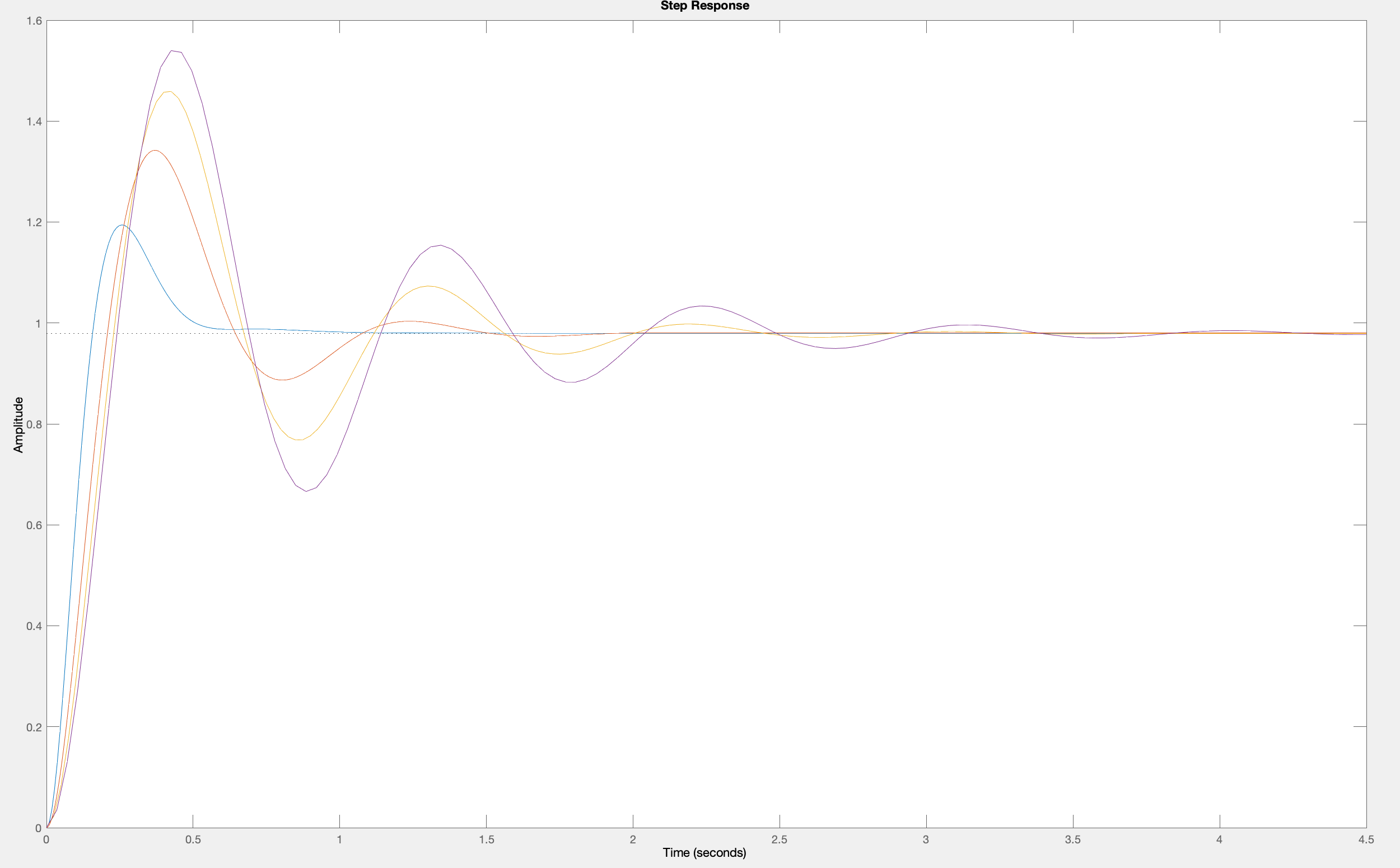
In the above plot, the step response for the s+4 controller has the smallest overshoot, unsurprising given the root locus plot. And what about the closed loop frequency response?
bode(feedback((240*(s+4)/((s+20)*(s*s+2*s+1))),1))
hold on
bode(feedback((120*(s+8)/((s+20)*(s*s+2*s+1))),1))
bode(feedback((80*(s+12)/((s+20)*(s*s+2*s+1))),1))
bode(feedback((60*(s+16)/((s+20)*(s*s+2*s+1))),1))
And the phase margin
margin(240*(s+4)/((s+20)*(s*s+2*s+1)))
hold on
margin(120*(s+8)/((s+20)*(s*s+2*s+1)))
margin(80*(s+12)/((s+20)*(s*s+2*s+1)))
margin(60*(s+16)/((s+20)*(s*s+2*s+1)))
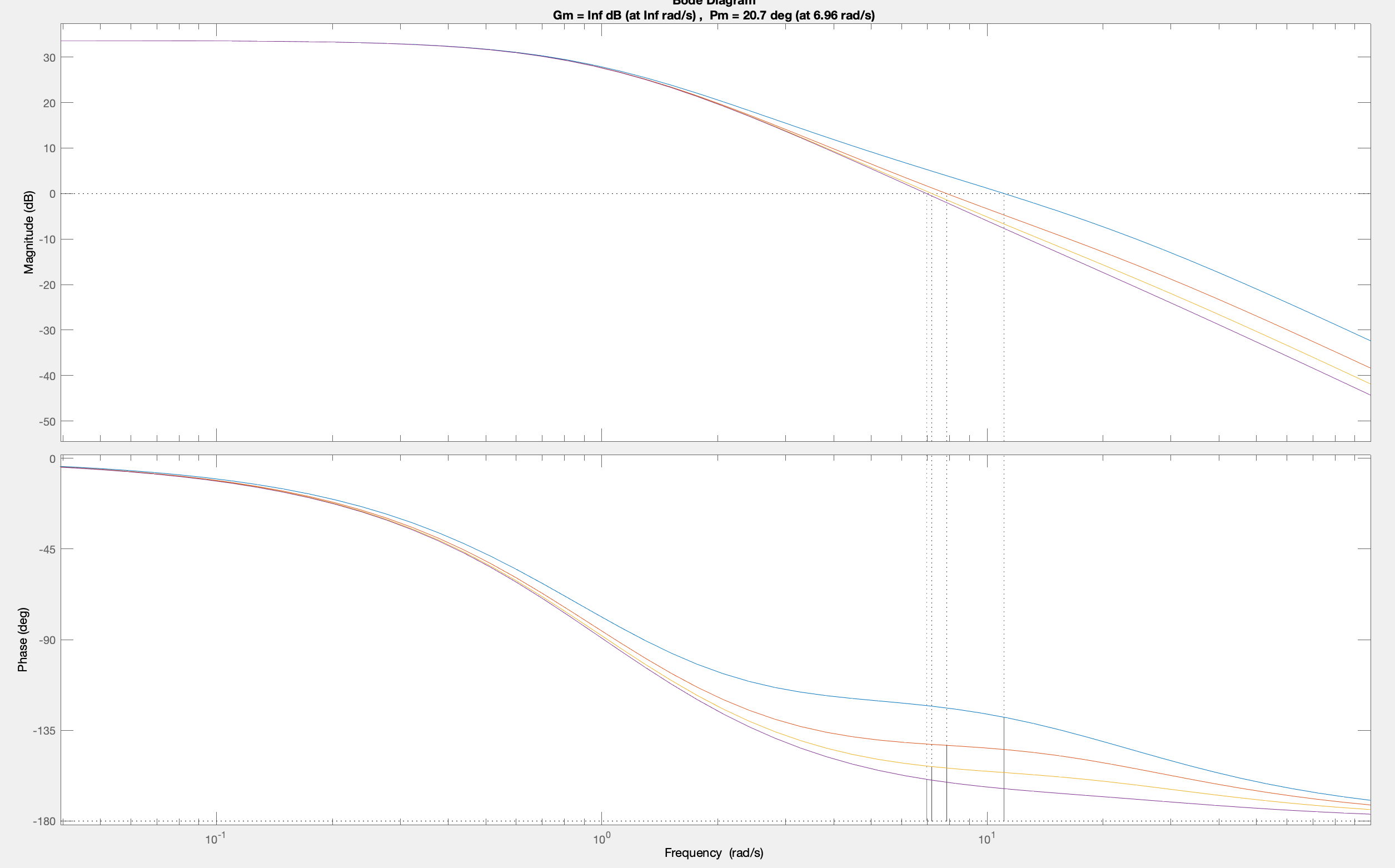
Notice that the s+16 controller resulted in a system whose step response had the most overshoot, whose frequency response had the most peaking, and whose phase margin was the smallest. Step response, closed-loop frequency response, and phase margin, they all they all tell the same story. The s+4 controller is more stable.
- exercises: Lead Compensation (Due Nov 03, 2023; 09:59 AM)
- exercises: Bode and Steps (Due Nov 03, 2023; 09:59 AM)
- exercises: Arm Like Example (Due Nov 03, 2023; 09:59 AM)
- exercises: Phase Margin (Due Nov 03, 2023; 09:59 AM)