A Disturbance in the Force

Quick Reference

NOTE

The new sketch, 6310_PROP_22_23_SWEEP, sets offsets for the values of K_d and K_p.

The offsets are specified on lines 40

#define offsetKd 0.2

and 42

#define offsetKp 0.5

When offsets are non-zero, they are ADDED to values from the plotter send window. For example, by typing "6 1.5" in the plotter send window to set a new value of K_p, 1.5 will be added to its offset of 0.5, and therefore

By typing "1 -0.1" in the plotter send window to set a new value of K_d, -0.1 will be added to its offset of 0.2, and

Send window values DO NOT ACCUMULATE! So if you type "6 1.5" in the send window, and then type "6 2.0", the resulting K_p will just be the offset added to the latest sent value, K_p = 0.5 + 2.0.

Serial Plotter Send Window Indices and offsets

Links

• Build instructions for adding second motor are at the end of section three in here.
• Sketch for this lab is here.
• Matlab script for week B is here.

Task Summary

Week A

1. Add second motor to your arm, download the new sketch, recalibrate angle sensor offset, and level the arm. (Checkoff 1).
2. Set K_i = 4.0 and find the smallest value of K_d for which the system is stable (step response settles to its steady-state in less than 5 seconds).
3. Measure the frequency of the oscillation in the step response, and the magnitude and phase of sinusoidal steady-state responses for several input frequencies.
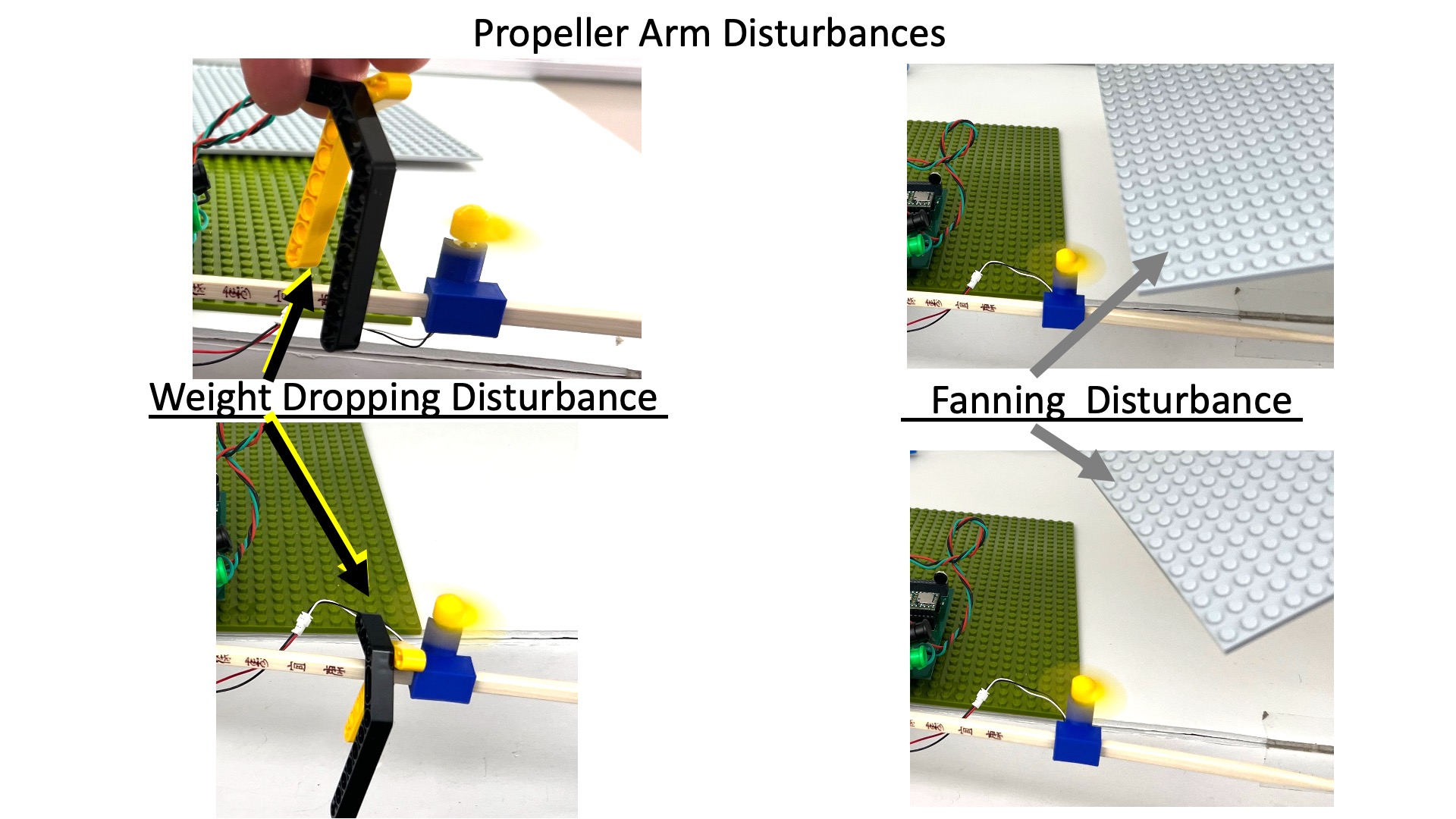
4. Disturb the arm by fanning it, and find the "fanning resonance frequency" that maximizes the disturbance response.
5. Consider how the following are related:
   • the frequency of the oscillations in the step response,
   • the frequency that maximizes the sinusoidal steady state response
   • and the frequency that maximizes the disturbance response (Checkoff 2).
6. Repeat 2->6 with K_i=0, K_p = 2, and for this case find a new smallest K_d for which the step response settles in less than five seconds(Checkoff 3).

Week B

Adjust \gamma_a and \beta in the provided matlab model so that the input-output frequency response of the model matches the steady-state magnitude and phase of your arm's input-output response at a few points.
Derive the disturbance to output transfer function, and update the matlab script (at the top of this page) so that it also computes the disturbance frequency response. Fan your arm to demonstrate that your model's disturbance frequency response accurately predicts the most disturbing frequency.
Use your model (and matlab) to design a controller with better disturbance rejection by examining the disturbance frequency response. Fan the arm to demonstrate the improved disturbance rejection of your better controller.

Double the Fun

Add a second motor (clip it into the counter-weight is on the right side of the arm, see the end of section three in the assembly guide). Connect both power supplies to the controller board and connect your laptop to the Teensy. Download the 6310_PROP_22_23_SWEEP sketch from the class web site (see link above), upload it to the Teensy, and start the serial plotter. Note that the sketch uses non-zero offset values for K_p and K_d, enough feedack that the arm should be close to level.

Transfer your angle sensor calibration (AngleOffset) BUT NOT THE NOMINAL COMMAND to the new sketch, and verify that the measured \theta_a is zero when you hold the arm level. Once the sensor is calibrated, adjust the black potentiometer (in the upper right hand corner of the board) to balance the right and left propeller forces so that the arm holds itself level.

Checkoff 1:

1. Show a staff member that your arm is functioning properly.

Ask for Help Ask for Checkoff Loading...

Steps, Sinusoidals and Interference.

Step response.

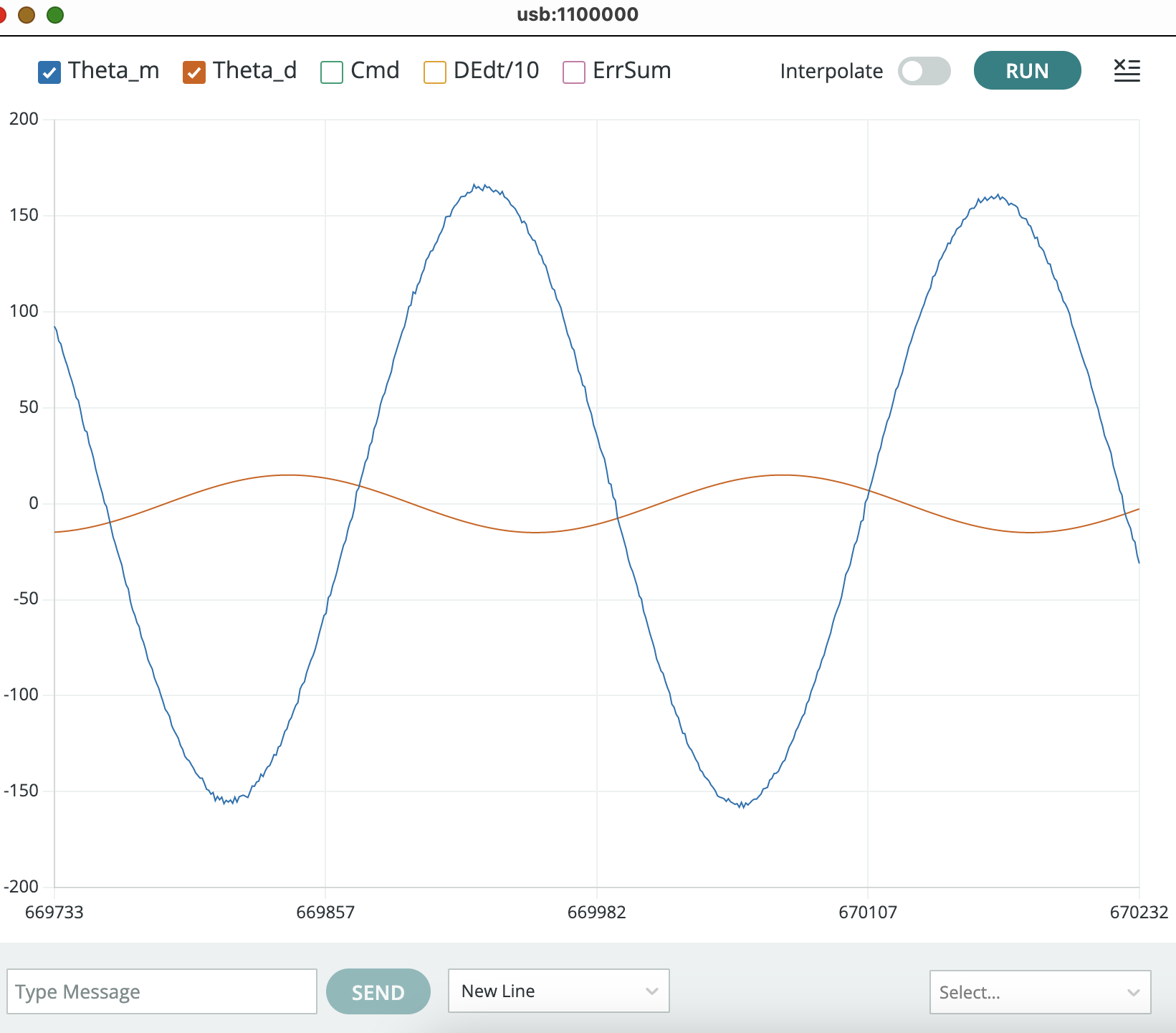
Set K_i = 4.0 by typing "2 4.0" in the plotter send window, and then type "6 0.1" and "5 0.1" to generate an input that toggles between -0.1 and 0.1 every 5 seconds (two transitions in a ten second period). Reduce K_d by typing, for example, "1 -0.1" in the plotter send window. Since a nonzero offset was specificed in the Teensy sketch, offsetKp = 0.2, adding -0.1 yields K_d=0.1. You should be able to find a K_d between 0.1 and 0.3, that results in step response similar to the one in the following video.

Notice that the step response plotted in the video above is barely stable, but it is stable! Try using your hand to perturb your arm by about 45 degrees, and then let it go. If your arm persists in oscillating wildly, and does NOT eventually level out, your arm is not stable enough, please increase K_d a little (ten percent) and try again.

Measure Frequency Response

In theory, measuring the frequency response of STABLE linear system is easy:

1. Pick a frequency and apply a sinusoid of that frequency to your system's input.
2. Wait for the system's natural responses to die out (they must die out eventually, since the system is stable). What remains will be sinusoidal at the same frequency as the input.
3. Compare the input sinusoid to the output sinusoid and compute the amplitude ratio and the phase difference.

We can measure the frequency response for our two-propeller arm system using the above approach as long as we are careful about three issues described below.

Monitor Motor Commands

While the two-propeller arm avoids the gravity-induced nonlinearity of the one-propeller arm, there is still a "clipping" nonlinearity that arises when the controller-generated motor commands exceed power supply limitations. This nonlinearity can usually be avoided by reducing the magnitude of the sinusoidal input, provided the clipping has been detected.

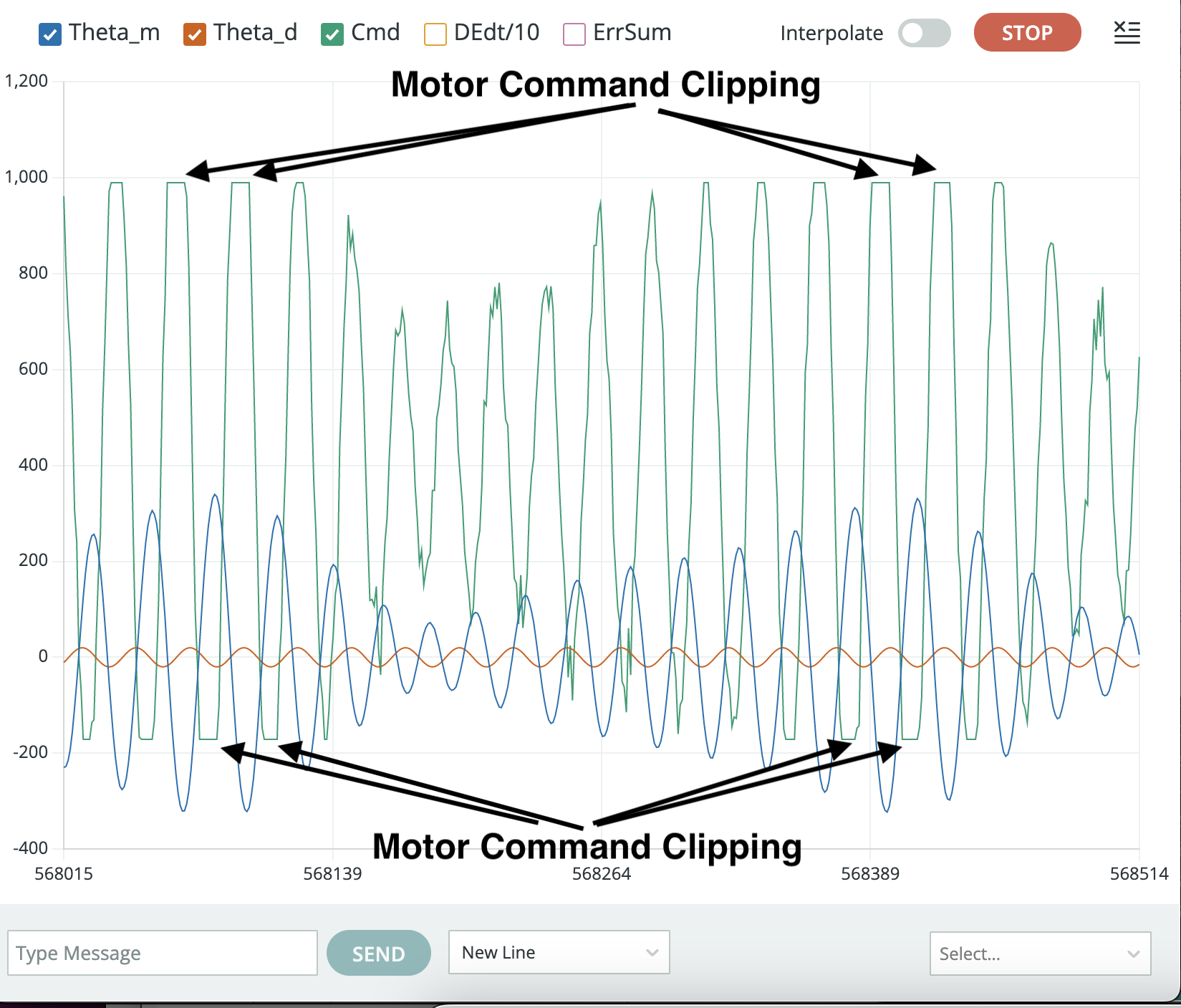
Monitor the motor command plot whenever measuring frequency response, to ensure the commands are not being "clipped" by power supply maximums. The clipping effect is easy to spot, as shown in the figure below. The black arrows point to cases where the motor command (the green curve) flattens, an indication that the controller's commands are being clipped because of power supply limitations.

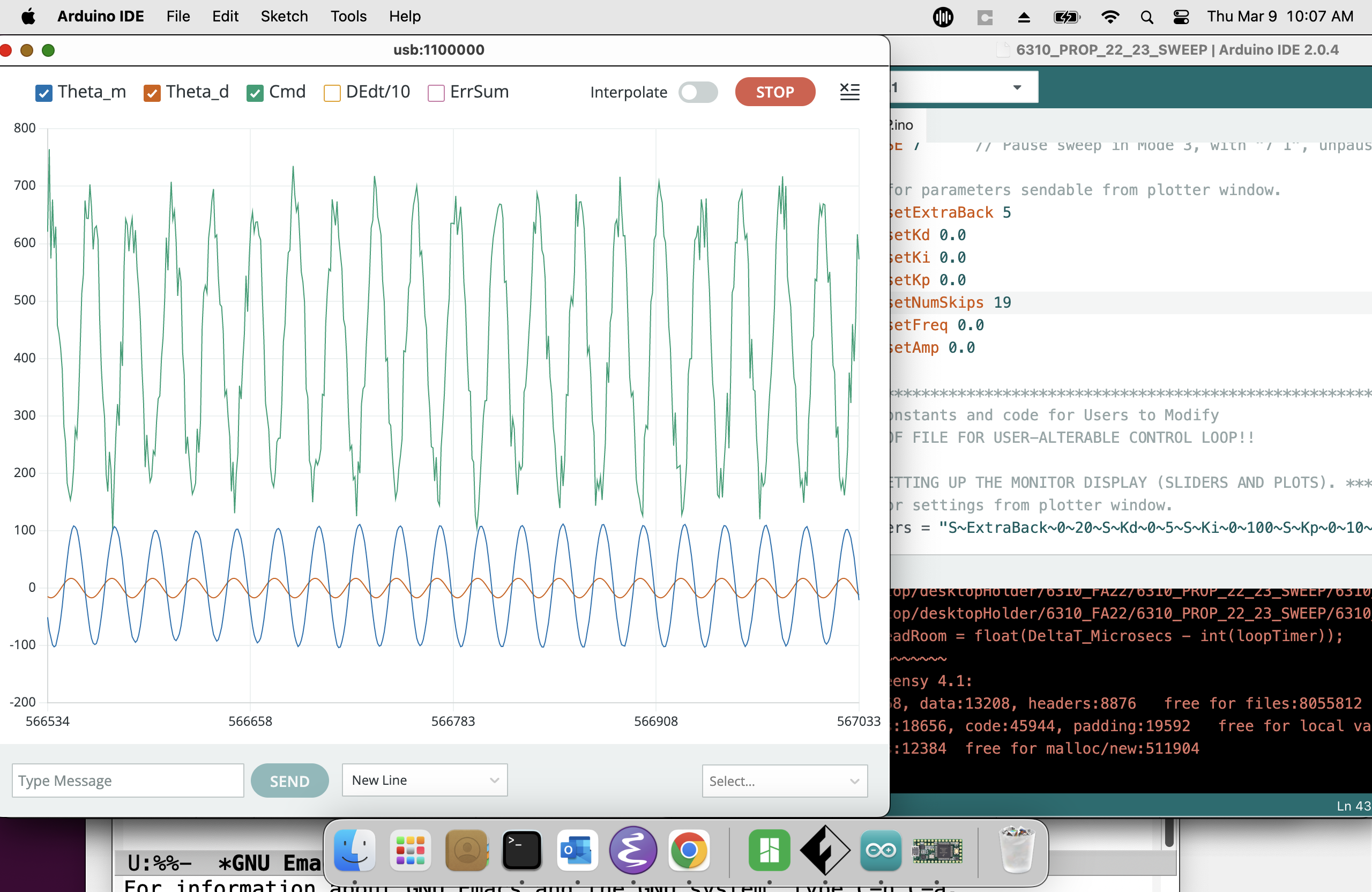
The clipping problem can usually be eliminated by reducing the input amplitude, as shown in the picture below. Avoid reducing the input amplitude too much though, because the microcontroller won't be able to represent the signal accurately. Reasonable sinusoidal amplitudes are values are between -0.04 to -0.07, and can be set using index 6 in the plotter send window. NOTE: USE NEGATIVE AMPITUDES, THE SKETCH WILL GENERATE STEPS INSTEAD SINES IF YOU USE POSITIVE AMPLITUDES.

Wait wait for Steady-State

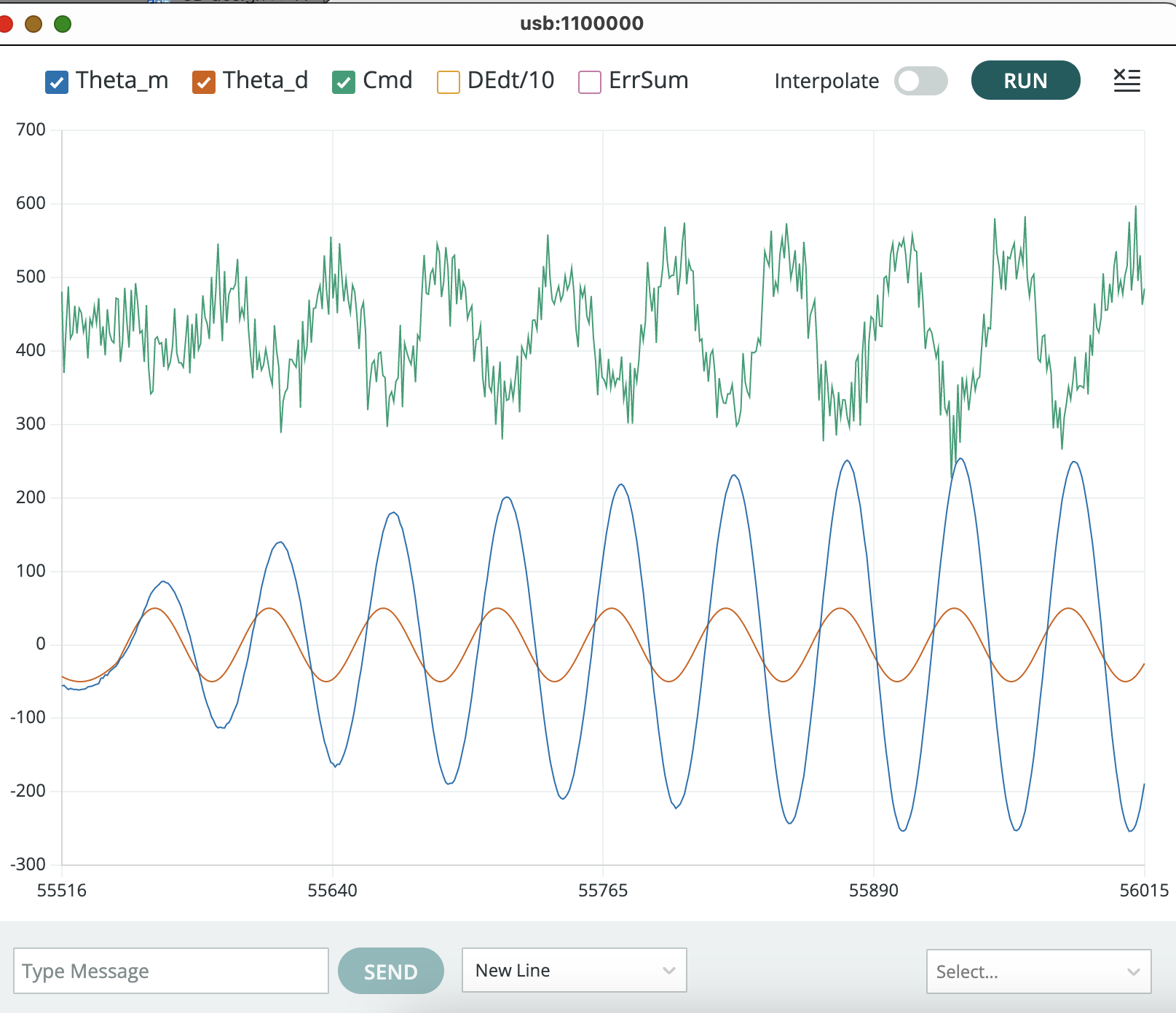
It can take several seconds to achieve sinusoidal steady-state, a typical case is shown in the picture below. Be sure to wait long enough (ten seconds or so) before pausing the plotter and taking measurements.

Spread Samples

The sketch default is to send an update to the serial plotter every 20 milliseconds, but you can decrease the time between updates and measure time more accurately. The fastest serial plotter update is once a millisecond (zero skips), to set that update rate, type "4 -19" into the plotter send window (as was done to generate the plot below).

Pushing the Arm's buttons

The simplest way to disturb the propeller arm is to generate extra air flow using a fan. A large building plate makes a good fan, but when you use it to disturb the arm, make sure you only fan ONLY ONE side of the arm (fanning both sides cancels most of the force). Try to find the fanning frequency that is most disturbing, but as you can see in the video below, finding the right frequency (while also aligning in phase) is not so easy to do.

Checkoff 2

For the second checkoff,

1. Measure the frequency of the oscillation in the step response, and the magnitude and phase of sinusoidal steady-state responses for several input frequencies.
2. Find the the input frequency that maximizes the amplitude of the output, and note the associated output's phase. How does phase change with frequency?
3. Draw a plot (with at least 10 points) of the magnitude and phase of the system's frequency response. How much does the magnitude and phase change at frequencies that are twenty percent above and below the frequency of the peak response?
4. Try disturbing the arm by fanning it, and find the "fanning resonance frequency," the frequency that maximizes the response.
5. Note the connection between the frequency the oscillations in the step response , the frequency that maximizes the sinusoidal steady state response, and the frequency that maximizes the disturbance response.

Checkoff 2:

1. With help from a staff member, follow the steps above.

Ask for Help Ask for Checkoff Loading...

Once again, without the integral.

Set K_i=0 by typing "2 0" in the send window, set K_p = 2 by typing "6 1.5" in the send window (see note about offsets at the top of this page), and adjust K_d so that you get a "barely stable" step response like in the video below.

Try fanning your updated system, you should be able to excite a resonance, like in the video below. As you can see in the video, at the faster resonance frequency, it can be even harder to "match up" to the resonance, please watch until (or skip to) the end to see what that looks like!!

Checkoff 3

For this checkoff,

1. Measure the frequency of the oscillation in the step response, and the magnitude and phase of sinusoidal steady-state responses for several input frequencies.
2. Try disturbing the arm by fanning it, find the "fanning resonance frequency" that maximizes the response.
3. Note the connection between the frequency of oscillations in the step response, the frequency that maximizes the sinusoidal steady state response, and the fanning frequency that maximizes the disturbance response.

Checkoff 3:

1. With help from a staff member, follow the steps above.

Ask for Help Ask for Checkoff Loading...

STOP HERE FOR WEEK A!!!!

Continuous Time (CT) Modeling

Last lab we derived an approximate discrete-time (DT) model for the innately continuous-time (CT)propeller arm. We chose discrete-time partly to match our innately discrete-time Teensy-based controller, and partly because discrete-time models, at least the ones formulated as systems of linear difference equations, have explicit solutions in the form of easily computed sums. For this and the next few labs, we will do the reverse. That is, we will derive CT models for innately-CT physical artifacts, and create approximate CT models for our innately-DT controllers.

We are switching to CT because the concepts we are exploring next, transfer functions and frequency response, have a simpler and more intuitive description in CT. And that simplicity will allow us to gain new insights into control system design.

Doubly-Driven Arm

Recall the functional diagram of the singly-driven arm from the first propeller-arm lab, repeated below.

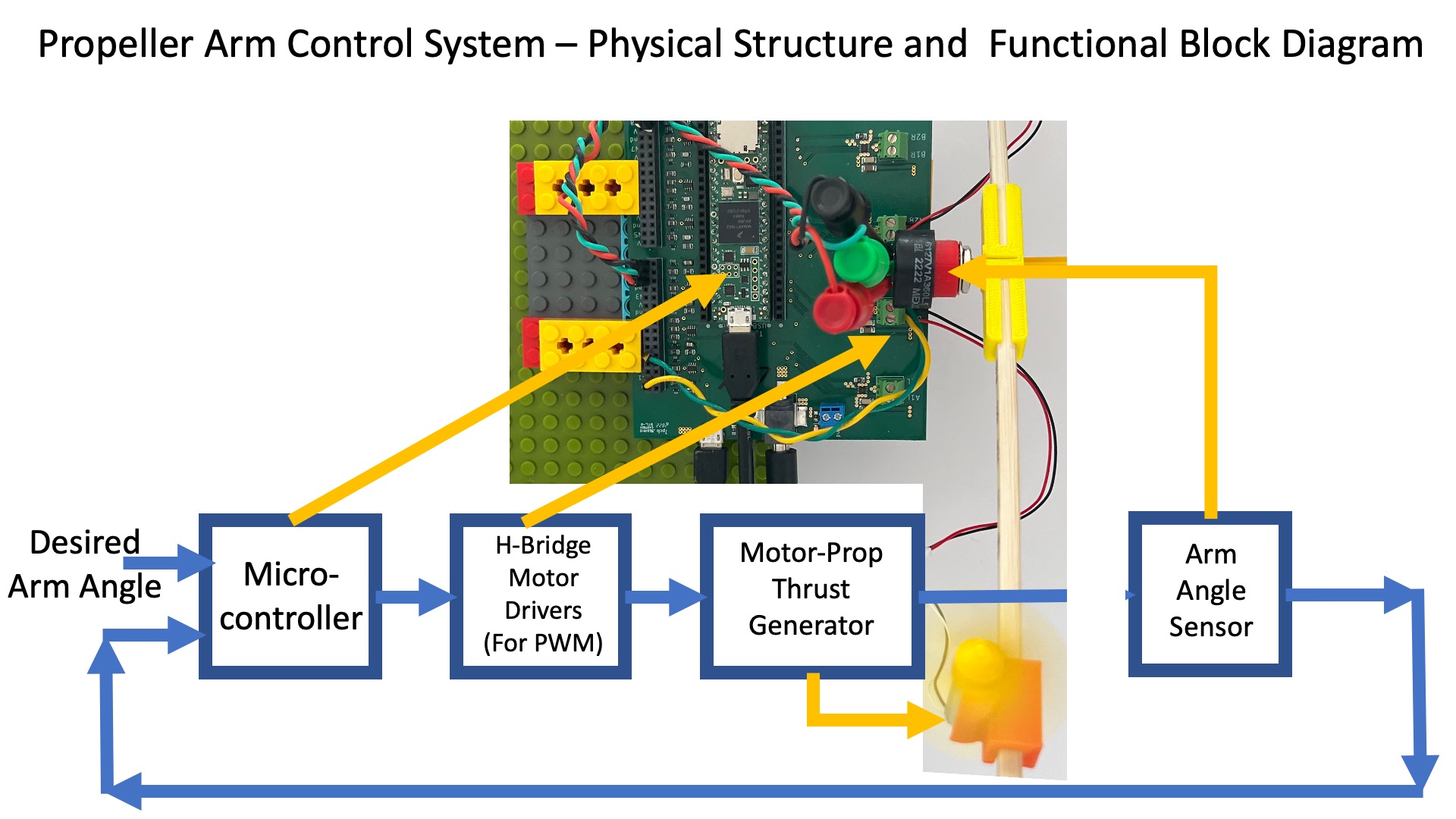
The above functional block diagram only points out thrust generation from one motor-propeller, showing both makes for an awkward picture. Instead, the set of forces and torques for the doubly-driven arm are best depicted in a more abstract form, as in the figure below.

In the above figure, we repeat the definitions of measured and desired arm angles, \theta_a and \theta_d, respectively, show the motor gravity and thrust forces, F_{nom}, f_{thrust}, and F_{gravity}^M, as well as the motor commands, C_{nom} and c. We also explicitly introduce the arm torque, \Gamma_{thrust}, due to the difference in right and left motor thrusts.

In the last lab, we did not model disturbances, and implicitly assumed the net torque on the arm was due to motor thrust alone. Under that assumption, \Gamma_{thrust} was an unnecessary intermediate in the relation between motor command and arm acceleration. This lab is focussed on modeling disturbances, and since our example disturbances (fanning and dropping weights) are torques, their effect on arm acceleration will be easier to model if we can add them to an explicit \Gamma_{thrust}.

Discrete-Time (DT) to Continuous Time (CT)

In the first propeller-arm lab, we related the change in arm angle, \theta_a, to the arm angular velocity, \omega_a,

an approximation to the CT differential equation,

Similarly, we related the change in arm angular velocity to the arm angular acceleration, \alpha_a,

an approximation to the CT differential equation,

Block Diagrams

Simple Model, Simple Control

In our simplest arm model, angular acceleration is assumed proportional to motor command, and in the simplest controller, the motor command is assumed proportional to angle error. In discrete time,

and in continuous time where K_p is the gain of the proportional feedback.

Note that the DT and CT equations are almost identical, the only difference it the replacement of [n] by (t)? Is that generally true?

We can combine the equations for the arm, from the previous section, and the equations for the motor and controller, above, into DT and CT block diagrams. The DT block diagram is in the figure below.

As we should expect, the DT block diagram uses delays and \Delta T blocks to model the difference equations.

The CT block diagram is shown in the figure below.

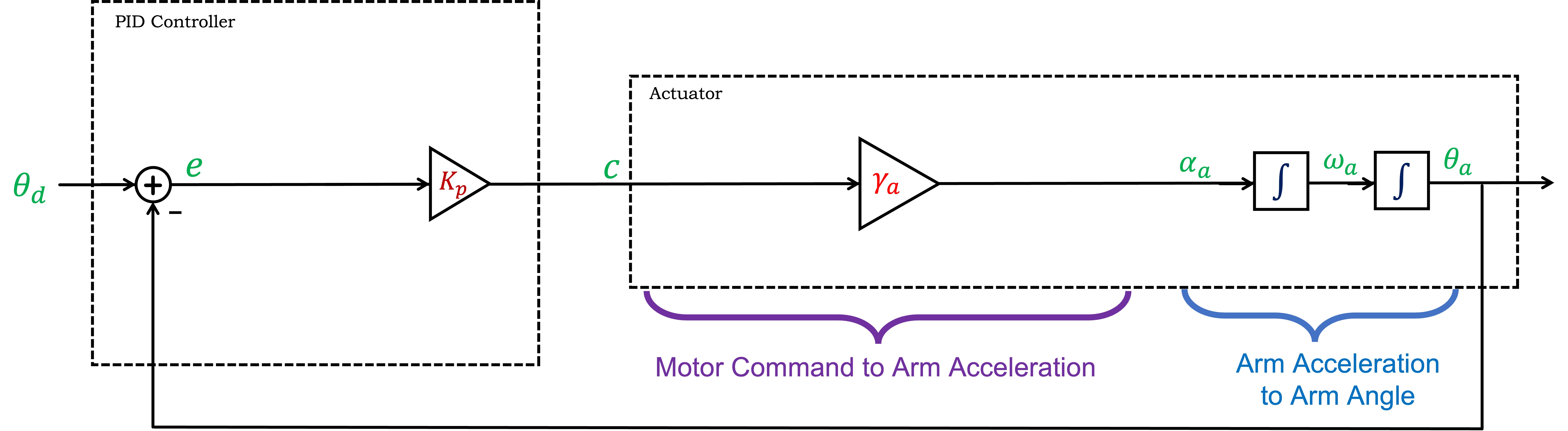
Note that in the CT diagram, we combined blocks with integral operators rather than combining blocks with derivative operators, a choice that parallels our intuition. That is, the system's controller sets the acceleration, which integrates to velocity, which in turn integrates to position, which we then measure and feed back.

Simple Model, PID control

We know that proportional feedback alone can not stabilize the propeller arm, so derivative feedback is essential, and we also know that integral feedback improves steady-state tracking. If all three (P,I,D) are included in a DT block diagram, the integral of the error will be approximated by a running sum of past errors scaled by the sample period, \Delta T, and the derivative will be approximated by error differences, scaled by \frac{1}{\Delta T}, as shown in the block diagram below.

In a CT block diagram, integral and derivative blocks can be used directly, leading to the much simpler block diagram shown below.

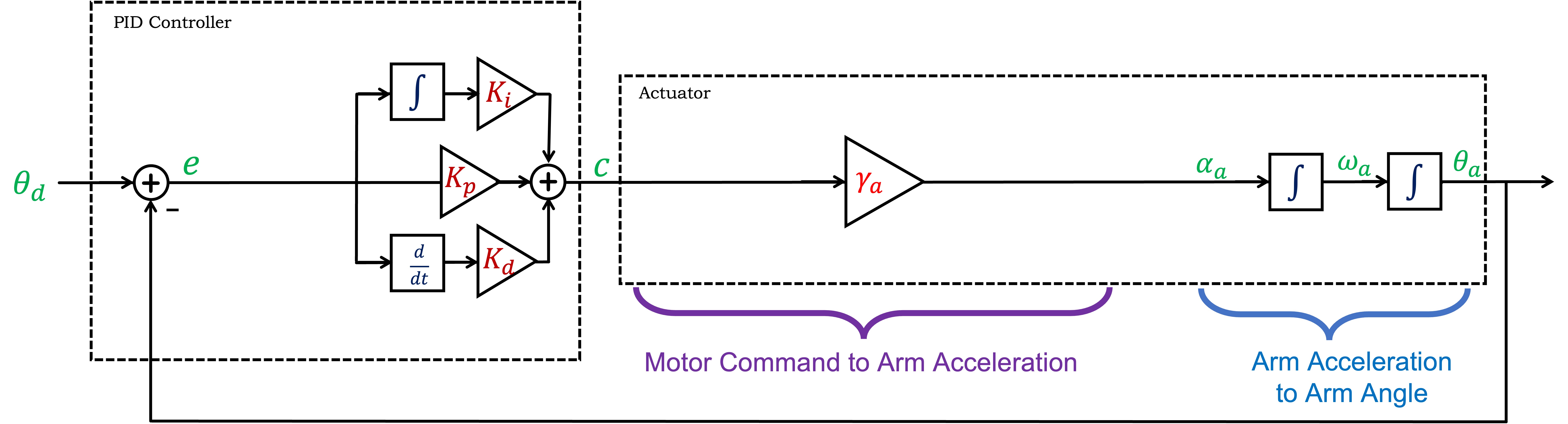
Even though the CT block diagram is simpler, ONLY the block diagram and associated model is simpler. The derivative and integral terms will still be approximated on the microcontroller using scaled angle error differences and running sums. But a simpler model represented by a simpler diagram is EXACTLY THE POINT. We are switching to CT because we use block diagrams to develop intuition and insight, so the fact that approximating DT controllers with CT models generates simpler diagrams than approximating CT physical systems with DT models is a BIG plus.

Non-instant Motor Model

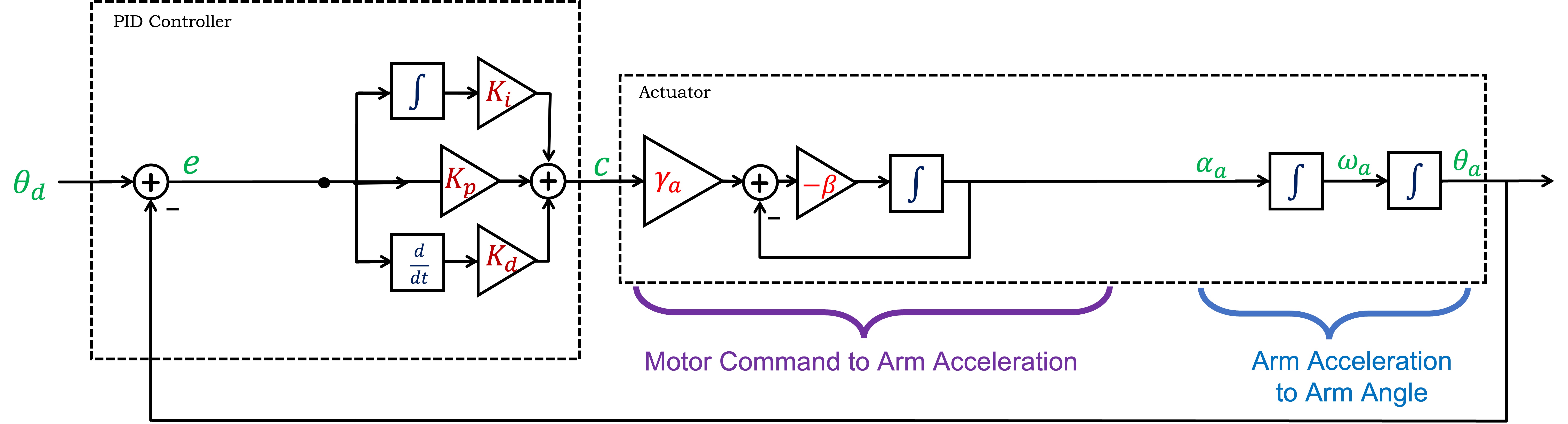
As we saw in the first propeller-arm lab, a more accurate model for the relationship between motor command and arm acceleration is

where \beta is assumed negative. Adding this better model to the DT block diagram yeilds the figure below.

Reorganizing the above difference equation

leads to an analogous differential equation, Adding the motor model to the CT block diagram leads to the figure below.

Using CT Transfer functions

In this lab we are transitioning from DT, difference equations and system functions that are ratios of polynomials in z^{-1}, to CT, differential equations and system functions that are ratios of polynomials in s. That is,

key identity: delays to z^{-1} \rightarrow integrals to \frac{1}{s},

for the actuator: H(z) \rightarrow H(s),

for the controller: K(z) \rightarrow K(s),

and for the feedback system: G(z) = \frac{K(z)H(z)}{1 + K(z)H(z)} \rightarrow G(s) = \frac{K(s)H(s)}{1 + K(s)H(s)}.

CT Advantage

Our design approach in discrete-time has been to minimize steady-state errors, by maximizing K_p, while maintaining stability,

We could follow the same path in continuous-time, minimizing steady-state errors by maximizing K_p while maintaining stabilility, But, then switching to CT would be about trading the stability region for DT poles, the interior of the unit disk, for the stability region for CT poles, the open left-half plane. And that does not seem worth the effort.

Switching to CT is not just about replacing z with s, we are making more than a ...symbolic... change. We will also change our approach to designing controllers. As we will see over the next few weeks, we can design good controllers if we know the actuator's frequency response (its sinusoidal-steady-state response to a sinusoidal inputs as a function of frequency). And in CT, if the poles of H(s) are stable, then the sinusoidal steady-state response to a sinusoidal input (in the form of a complex exponential),

is given by where H(j \omega) = H(s)|_{s = j \omega} and \omega = 2 \pi f is the frequency in radians/second.

Arm Block Diagram using System Functions

Replacing the integrals in the CT block diagram with \frac{1}{s} is the first step in using system functions, as in the diagram below.

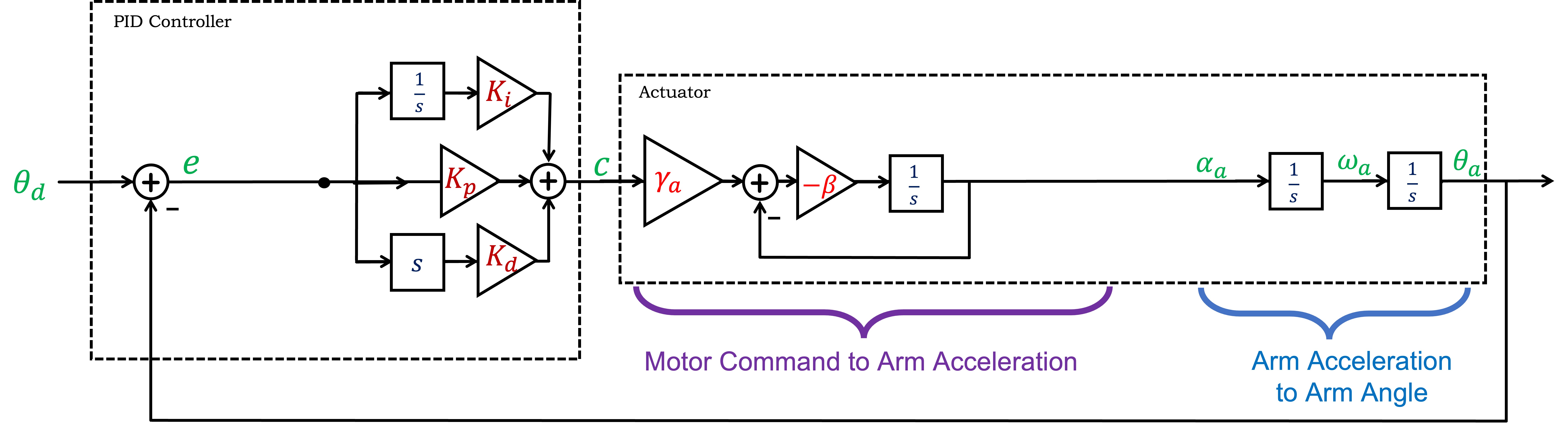
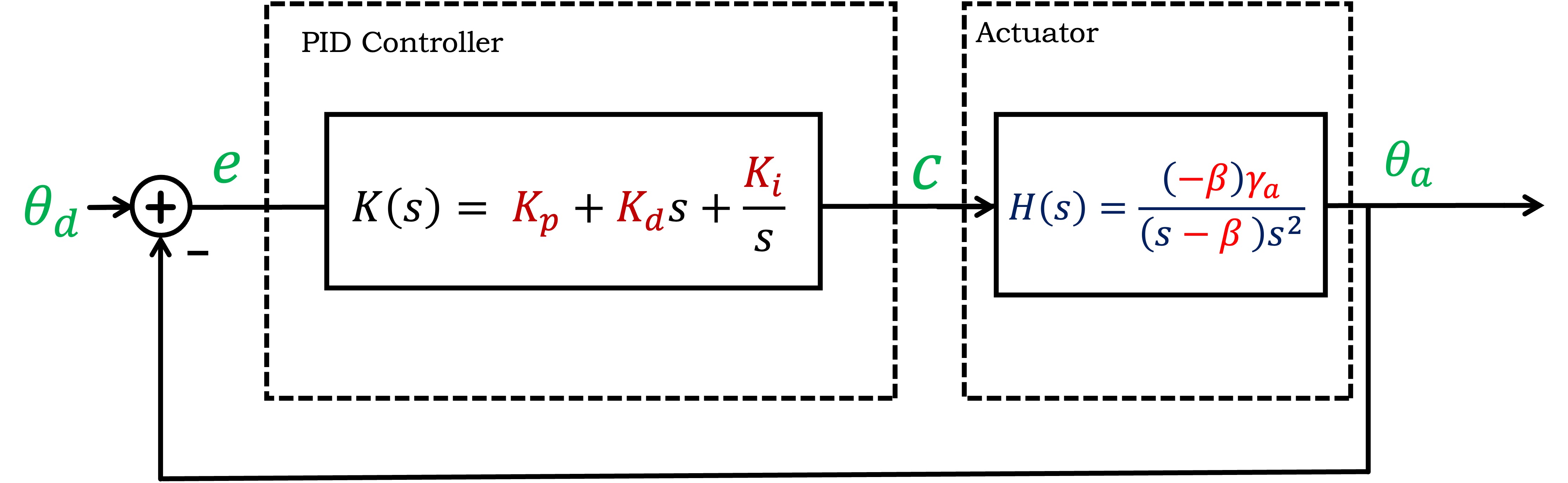
Blocks described by system functions can be composed by multiplication, allowing us to simplify the arm block diagram into two system functions, K(s), the controller, and H(s), the actuator, where each is a ratio of polynomials in s, as shown below.

Matlab Tools for CT and Frequency Response.

You can use matlab to manipulate continuous-time transfer functions, but there are a few differences between s- and z-domain manipulation. First, you have to tell matlab to use s as the CT transform variable, by typing

>> s = tf('s')

After that, you can define a CT transfer function. For example, suppose your system is described by a set of differential equations

then where H(s) is the CT transfer function given by

In matlab, if you type

>> H = (1/(s+0.1))*(1/s)*(1/s)

Matlab will response with

H =
 
        1
  -------------
  s^3 + 0.1 s^2

Then if you type

>> pole(H)

matlab will respond with

ans =

         0
         0
   -0.800

as you would expect since in CT, two of your poles are at zero.

Many of the matlab commands you've used before translate in the obvious way (feedback, step, etc), and we will also make extensive use of the bode command

bode(H)

For example, consider a system with input x(t) and output y(t) described by a first-order differential equation,

where y is the output and x is the input. Suppose we know that x(t) = \cos(\omega t) = \cos(2\pi f t) where \omega is the frequency in radians per second and f is the frequency in cycles per second. Approximately what is y(t) in the limit as t \rightarrow \infty ?

The system function is easy to compute using the techniques described in the prelab, and is H(s) = \frac{1000}{s+1}. If x(t) = u(t), the unit step, then x(t)=0 for t < 0, and x(t) = 1 for t \ge 0. To plot the response to the unit step using matlab, in the command window type (be sure you have defined s to matlab using s = tf('s')).

H = 1000/(s+1)

to define the system function to matlab, and then

step(H)

to plot y(t) given x(t) = u(t). Note that y(t) rises to 1000 with a time constant of one second (about two-thirds of the rise in one second).

The frequency response of this first-order system can be plotted using

bode(H)

If we use unity-gain feedback with this first order system, then

and by using K(s) = 1 in Black's formula, the closed-loop system function, G(s), is given by which matlab can determine for us using the feedback commandt

G = feedback(1000/(s+1),1)

To plot the step response of the feedback system,

step(G)

The frequency response also shows the impact of including the first-order system in a closed loop, as can be seen in the plot generated by

bode(G)

What is different about the open-loop to the closed-loop step and frequency responses?

If we want to determine y(t) given x(t) = \cos{\omega t} in the limit of large t (what we call sinusoidal steady state), we can use the frequency response. That is,

The magnitude and angle of G(j\omega) can be determined from the Bode plot, as as shown in the figure below.

Determining response at a particular frequency from the Bode plot.

Checkoff 4 - Calibrate the model

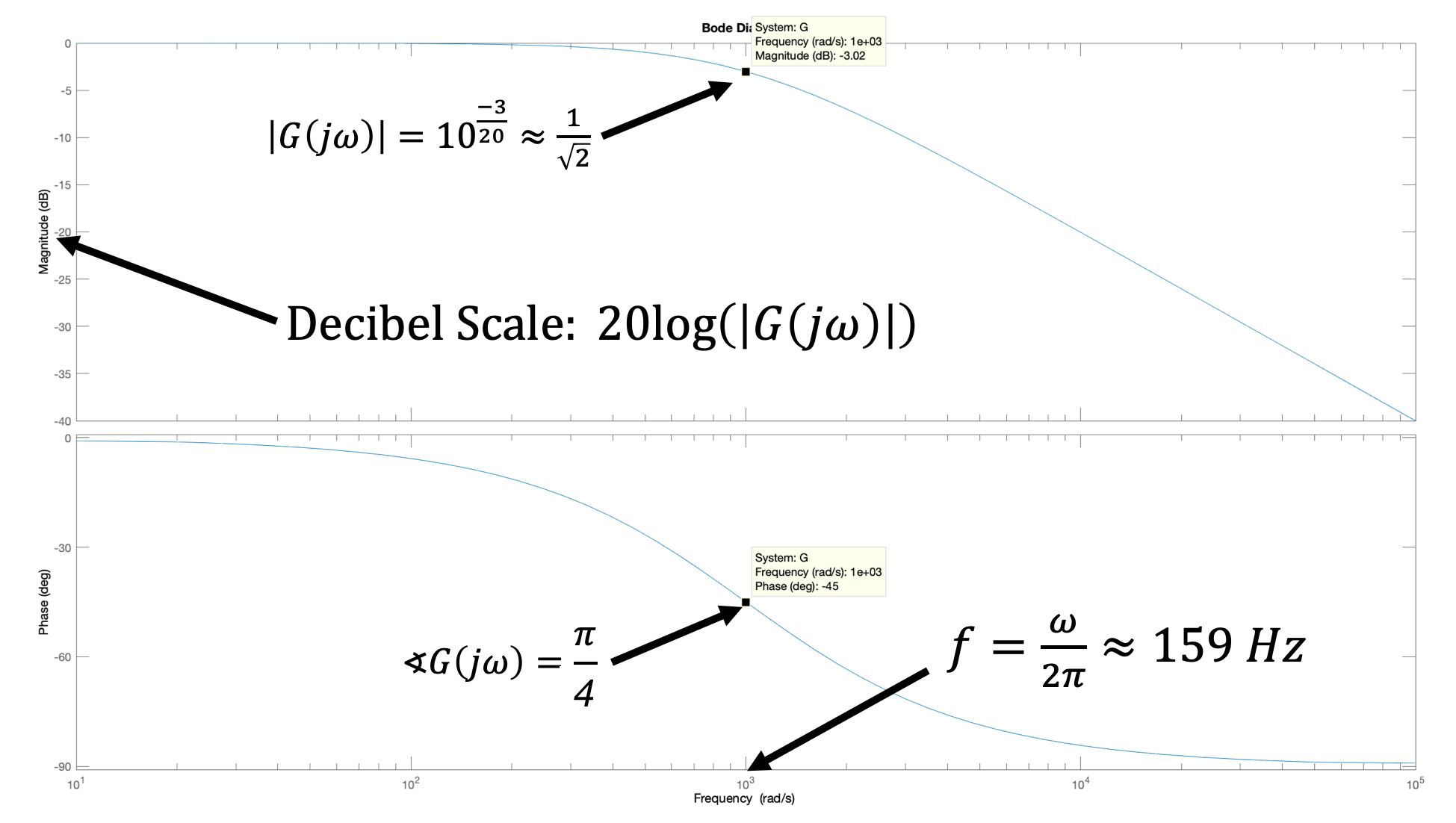
To get you started, we wrote a matlab script with the CT closed-loop system transfer function, nominal values for the coefficients and a weak controller, HERE. Running the script should produce plots like the ones below, showing the standard bode plots, our rescaled versions, and the system step response.

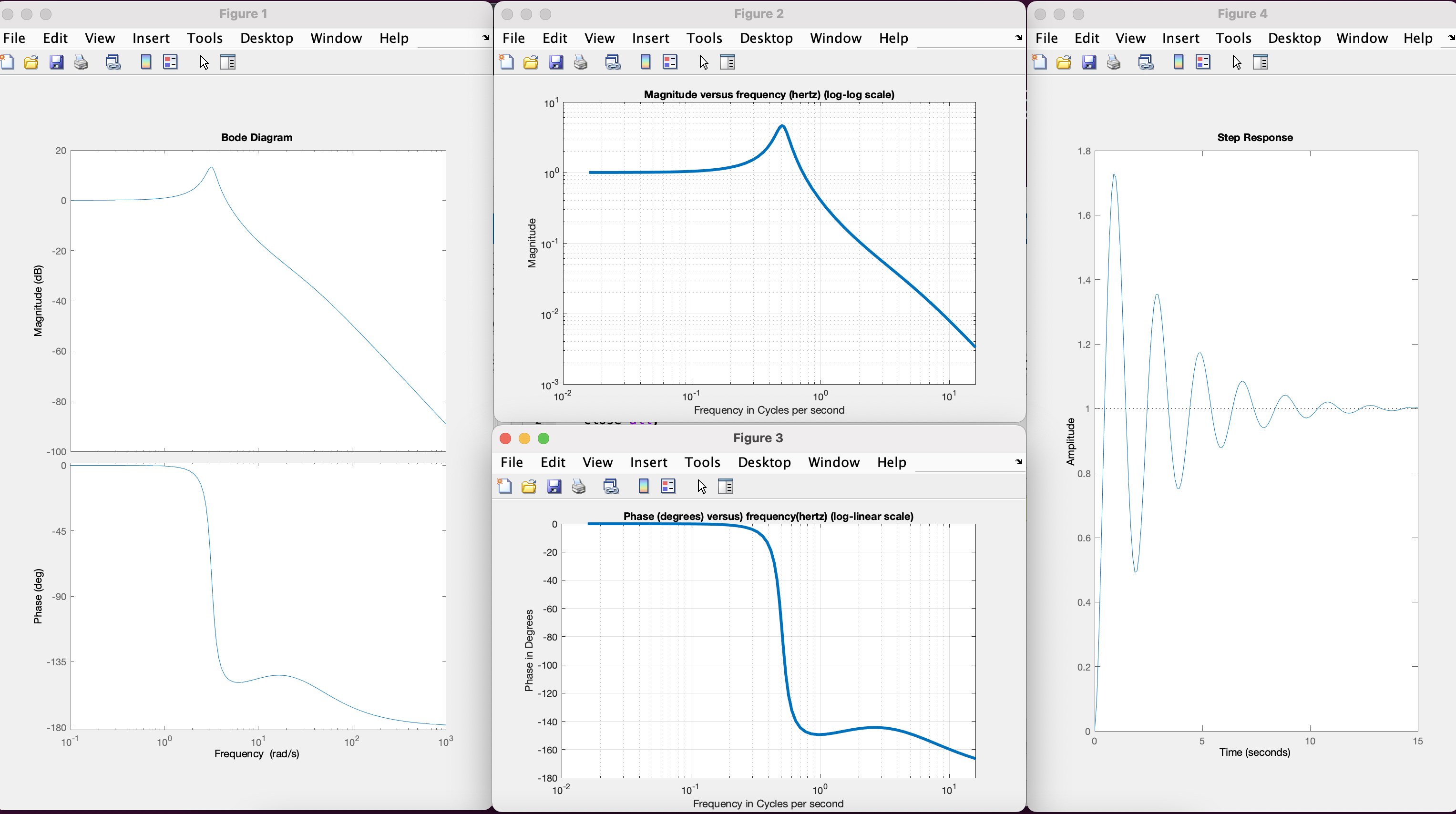
Use our script to plot frequency response, and compare the predicted and measured magnitude and angle of the response of your arm at a variety of frequencies. Adjust the parameters, \beta and \gamma_a of the matlab model to get good matches over a range of controller gains and frequencies.

Checkoff 4:

• For the two sets of controller gains you used last week, show, by measuring the response to sinusoids at a few different frequencies, that you picked good values for \gamma_a and \beta in the matlab models.
• Look particularly carefully at the frequencies corresponding to peaks in the system's responses for each gain set. How well did the model and measured magnitudes and phases match?

Ask for Help Ask for Checkoff Loading...

Disturbing Problems

For the propeller arm, we have examined two example disturbances, dropping weight and fanning, as shown in the image below.

Adding disturbance torques (generated by dropping or fanning) to the abstracted description of arm leads to the image below.

Disturbance torques can be added to the CT block diagram, but as we mentioned above, the simplest approach is to introduce torque as an intermediate variable, as shown below.

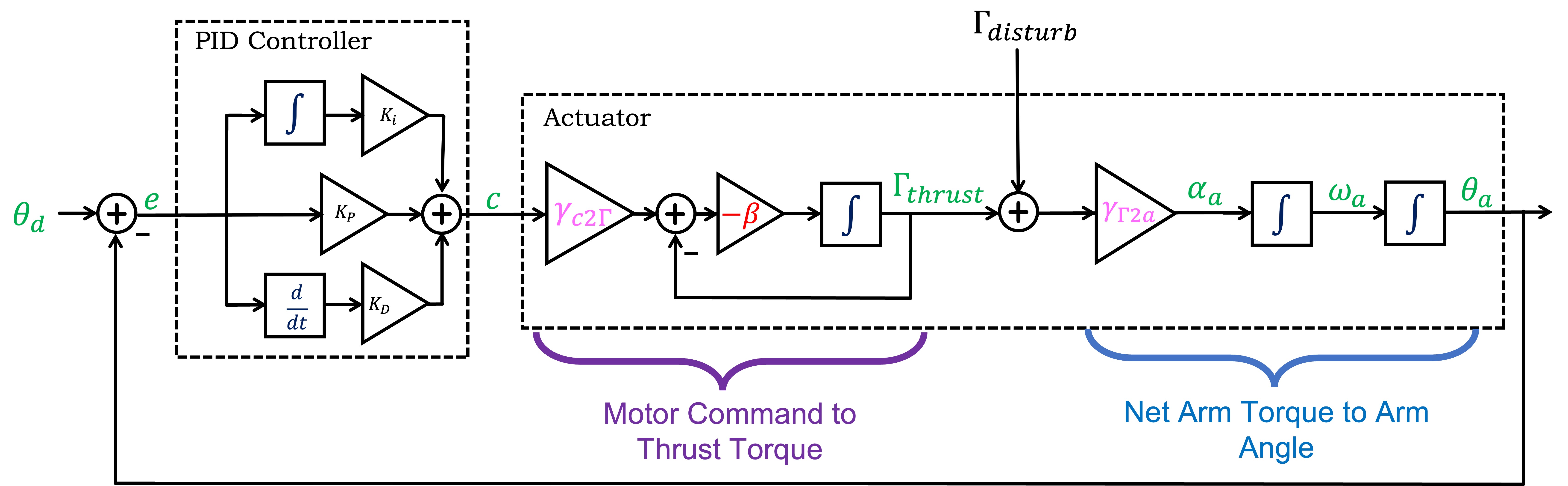
Notice that we introduced \Gamma_{thrust}, the net thrust torque generated by the motor-propeller pairs, and added a disturbance torque, \Gamma_{dist} (as might be generated by "dropping" or "fanning"). The sum of torques is then scaled to produce arm angular acceleration. Notice also that we replaced \gamma_a with \gamma_{c2\Gamma} and \gamma_{\Gamma 2a} (unfortunate because you just calibrated \gamma_a, but there is a fix).

As a hint to how to recover your calibration, consider manipulating the block diagram as shown below. Is the overall scale factor for the disturbance torque important?

Checkoff 5:

• What is G_{disturb}(s), the transfer function from disturbance to arm angle?
• Modify the matlab to plot the disturbance frequency response. Do you need to recalibrate your model if you are unconcerned about the absolute scaling of the disturbance?
• Show that you can predict the frequency of maximum disturbance using your model.

Ask for Help Ask for Checkoff Loading...

Checkoff 6 - Design a less disturbable controller

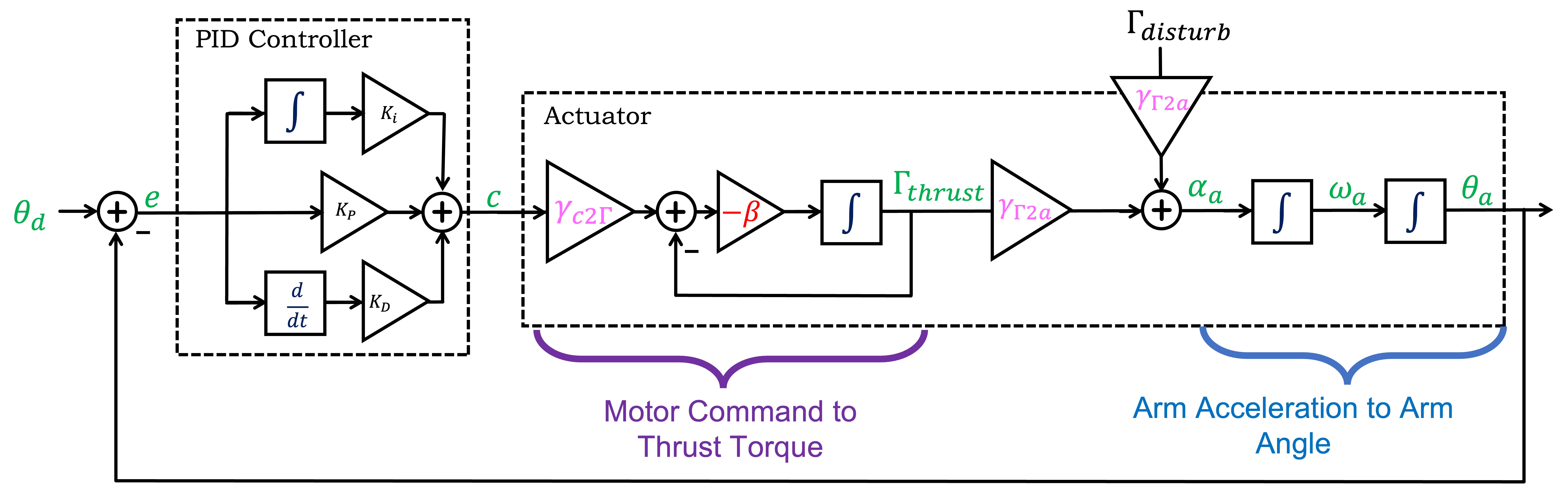
Now that you have a calibrated matlab model for your system, and can use the model to plot G_{disturb}(j\omega) (to within a scale factor), you can pick K_p, K_i and K_d to minimize the maximum disturbance response. Please do so, and show that your new controller is less "disturbable".

Checkoff 6:

• If K_i > 0, what can you say about the disturbance frequency response?
• If you double both K_p and K_d, how does your measured and modeled disturbance frequency response change? Pay particular attention to the peak response frequency.
• Collect sweep data for arm by following the instructions for running a sweep in the resource guide.

Ask for Help Ask for Checkoff Loading...