Linear Differential Equations and Complex Exponentials
Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.
(Adapted from notes by T.F. Weiss)
To outline what follows:
- A summary of the transition from DT to CT
- Sources of linear differential equations
- Homogeneous solution --- exponential solution, natural frequencies
- Particular solution --- system function, poles and zeros
- Total solution --- matching initial conditions.
- The system function, H(s), and its use in block diagrams.
We started in discrete time, using linear difference equations (LDEs) to model motor and arm behavior. In continuous time, we replace difference equations with differential equations, replace shifts in index with derivatives in time, and replace integer index n with real scalar t. And we can begin by following a parallel path, starting with the fact that we can still refer to linear DIFFERENTIAL equations as LDEs. And just like in discrete-time, we can compute natural frequencies by substituting solutions based on assuming a parameterized form, e.g. x(t) = X e^{st}, which we plug into the LDE to determine parameters. And again, just like in discrete time, either approach relied on a key property, that derivatives of an exponential function are related by a scale factor. For example,
To begin to examine the parallelism between DT and CT, let us consider a fairly general high order LDE example.
In discrete-time, one general form for an LDE with input sequence x and output sequence y is
In continuous time, the general form for an LDE with input time function x and output time function y is
Plugging in x(t) = X e^{st} and y(t) = Y e^{st},
Given an input x(t) = X e^{s_0 t}, we can find a particular solution y_p(t) = Y e^{s_0 t}, then
For systems described by difference equations in DT or differential equations in CT, determining natural frequencies involves finding the (possibly) complex roots of the system's characteristic polynomial. Finding DT and CT natural frequencies may lead to similar computational problems (polynomial root-finding), but their impact onn behavior is definitely NOT similar.
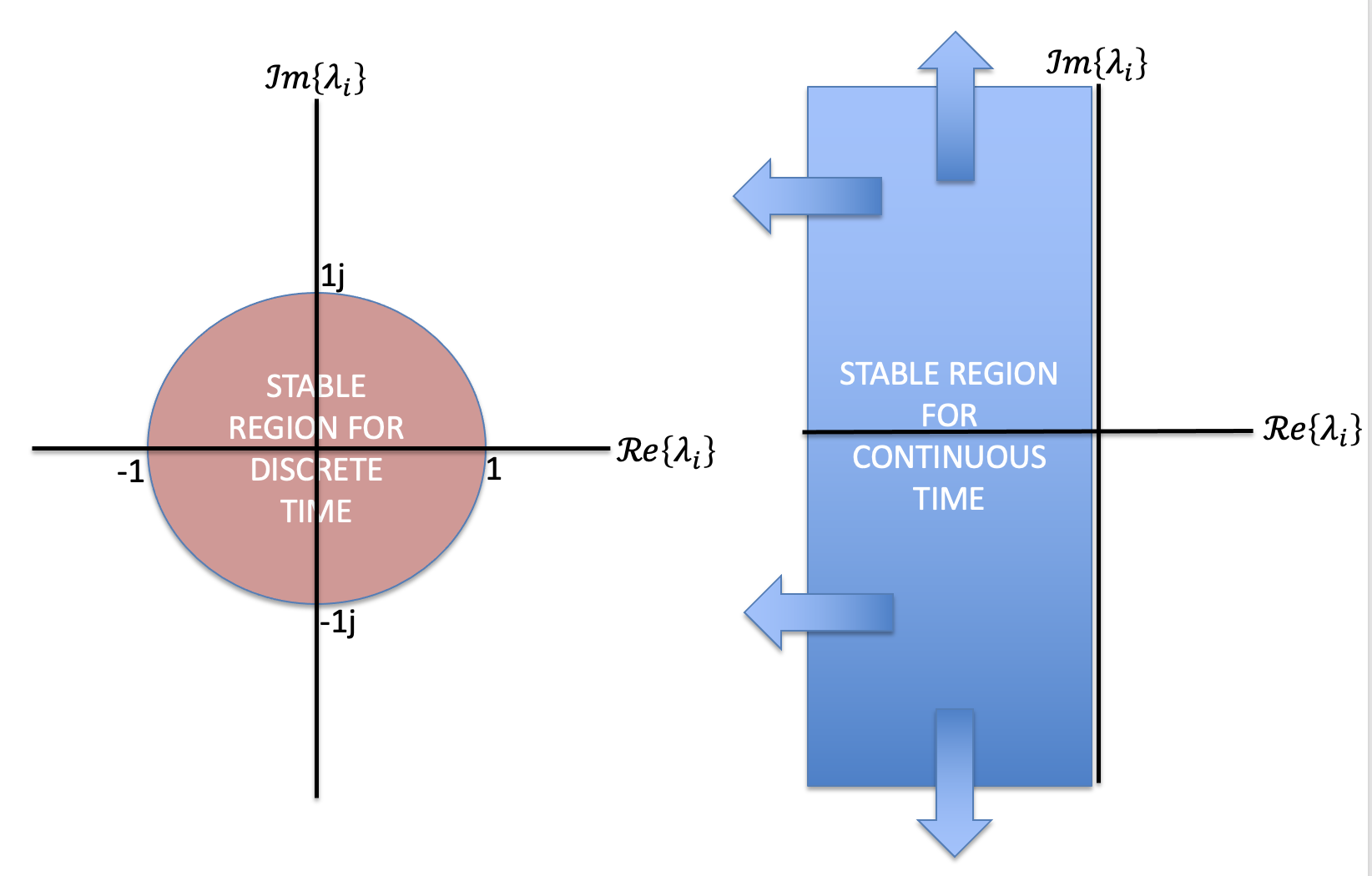
Of particular concern are natural frequencies that correspond to homogenous solutions that are growing (unstable), or decaying (stable). In discrete time, if all of a difference equation's natural frequencies are inside the unit circle, |\lambda_i| < 1 for all i, then since \lambda_i^n decays to zero for alli, the system is stable. In the continuous time case, if all the natural frequencies are in the left-half plane, \Re{(\lambda_i)} < 0 for all i, then e^{\lambda_i t} decays to zero for all i, and the CT system is stable.
To examine the behavior due to CT natural frequencies more closely, consider that a complex number \lambda can be written in real-imaginary or magnitude-angle form. That is,
In discrete time, natural frequencies are related to difference equation solutions through the power function. So if \lambda is a discrete-time system's natural frequency, then we are concerned with
In continuous time, natural frequencies are related to differential equation solutions through the exponential function. So if \lambda is a differential equation's natural frequency, then we are concerned with
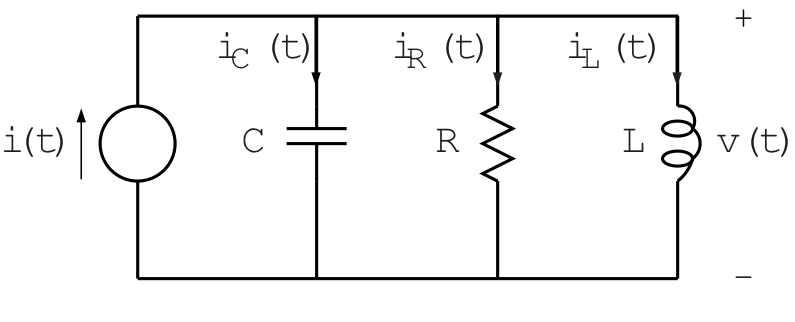
Kirchoff's current law yields
The constitutive relations for each element yield
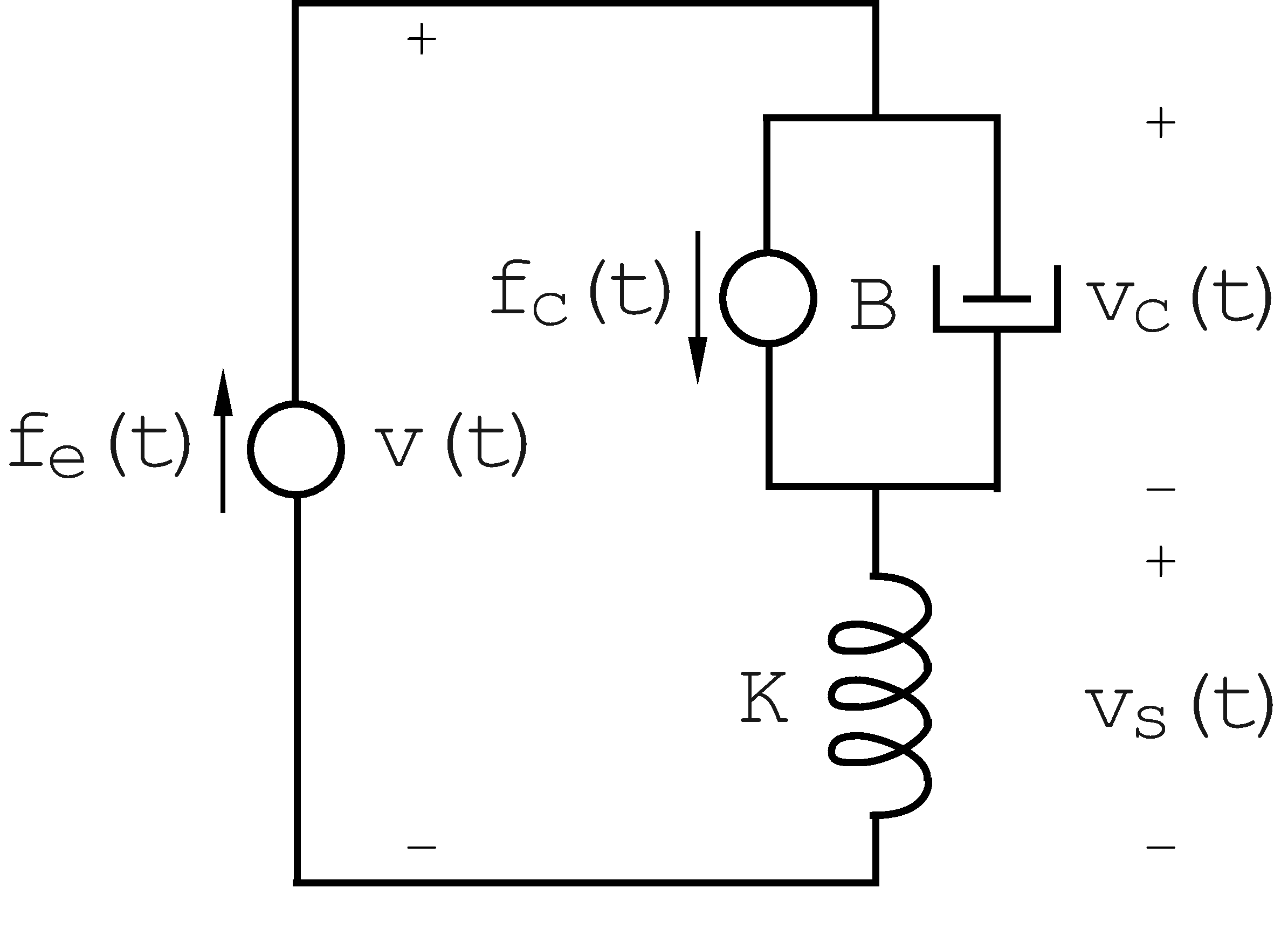
The simplest possible model of a muscle (the linearized Hill model) consists of the mechanical network shown below, in which the rate of change of the length of the muscle, v(t), is related to the the external force on the muscle f_e(t).
 u
uThe muscle velocity can be expressed as
A reversible,first-order chemical reaction can be represented as follows
For many "lumped" physical systems the input, x(t), can be related to the output, y(t), by an nth order differential equation of the form
When we studied difference equations describing discrete-time systems, we focused on computing solutions for two cases:
- The Zero Input, or Homogenous, case with non-zero initial conditions,
- The Step Response case, where the input is the time-shifted unit step and the initial conditions are zero.
Let the homogeneous solution be y_h(t), then the homogeneous equation is
The roots of the characteristic polynomial
Do not be confused by the tuning fork example, the vibration frequency is NOT a natural frequency. Since the fork's vibration eventually dies away, the natural frequencies associated with the vibration are a pair of complex numbers. Both have the same real part, a negative number that indicates the decay rate, and the same magnitude of the imaginary part (negative in one and positive in the other), which indicates the vibration frequency.
If the natural frequencies are distinct, i.e., if \lambda_i NOT equal to \lambda_k for all i not equal to k, then the most general homogeneous solution has the form

The differential equation relating v(t) to i(t) is
Now we need to find a particular solution to the differential equation
If we assume s_0 is NOT equal one of the natural frequencies, then
Substitution for both x(t) and y(t) in the differential equation yields, after factoring,
The relationship between the complex scalar Y and the complex scalar X depends on the frequency of the input, s_0, and has the form
The general solution to the LDE, given the input Xe^{s_0 t}, has a particularly simple form if we assume that the natural and input frequencies are unique,
Note that to completely compute the solution, we would need to determine the L coefficients
The total solution can also be computed using the unilateral Laplace transform, but as we will see in the following weeks, we will have little reason to investigate the impact of specific initial conditions.
- is called the system or transfer function,
- is a rational function in s,
- is a skeleton of the differential equation,
- characterizes the relation between x(t) and y(t).
Step to reverse the steps used to compute H(s) by cross-multiplying
In general, H(s) can be expressed in factored form as follows
- \{s_{z_1},s_{z_2},\ldots s_{z_M}\} are the roots of the numerator polynomial and are called zeros of H(s) because these are the values of s for which H(s)=0.
- \{s_{p_1},s_{p_2},\ldots s_{p_N}\} are the roots of the denominator polynomial and are called poles of H(s) because these are the values of s for which H(s)=\infty.
Note that poles of H(s) are the natural frequencies of the system. Recall that natural frequencies are given by the roots of the polynomial,
The system function, H(s), completely characterizes the differential equation, and H(s) is characterized by the location of L poles, \tilde{L} zeros, and an overall scale factor K. We can characterize how H(s) changes with s using a pole-zero diagram, a plot of the locations of poles and zeros in the complex-s plane. The ordinant is j\Im\{s\} = j\omega and the abscissa is \Re\{s\} = \sigma where
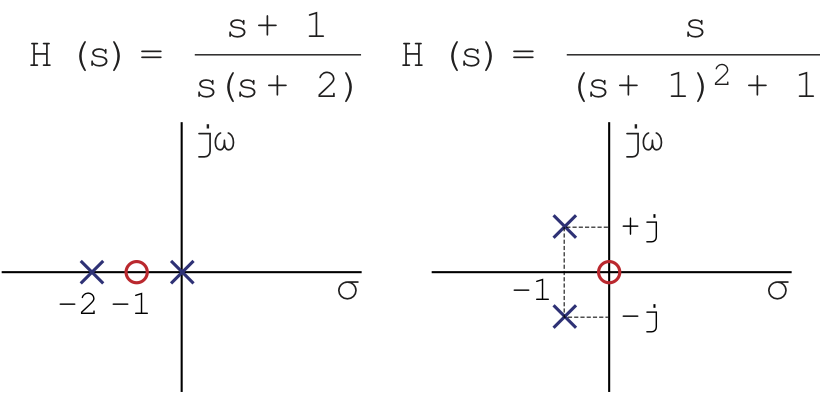

The differential equation relating v(t) to i(t) is
With v(t) as the output and i(t) as the input, the system function of the RLC network is
Given the system function
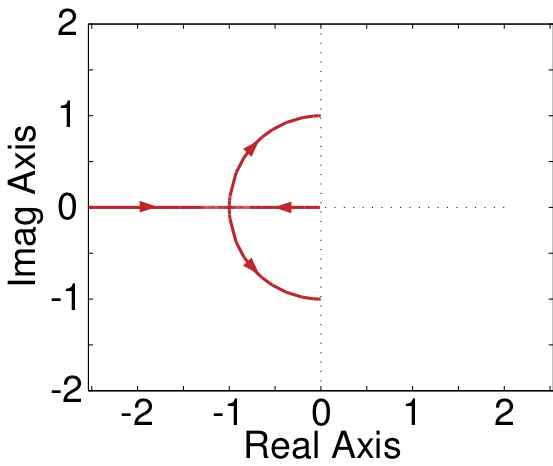
Solution
The natural frequencies of the system are the poles of the system function and are -3 and -4.
The differential equation can be obtained by cross multiplying and multiplying by e^{st} to obtain
An example structural description (e.g. a circuit):

where
There are many ways to compute LDE natural frequencies, and to compute LDE solutions given an input. If that is all we were doing, we would not need transfer functions. But suppose your system is a composition of smaller subsystems, in series or parallel, possibly surrounded by feedback? Given the transfer function description of each subsystem, you can easily compute the overall system function, a computation that will only involve forming products, sums and ratios of the subsystem transfer functions.
In the figure below, we note some examples of composition: parallel sum, sequential application, and feedback.
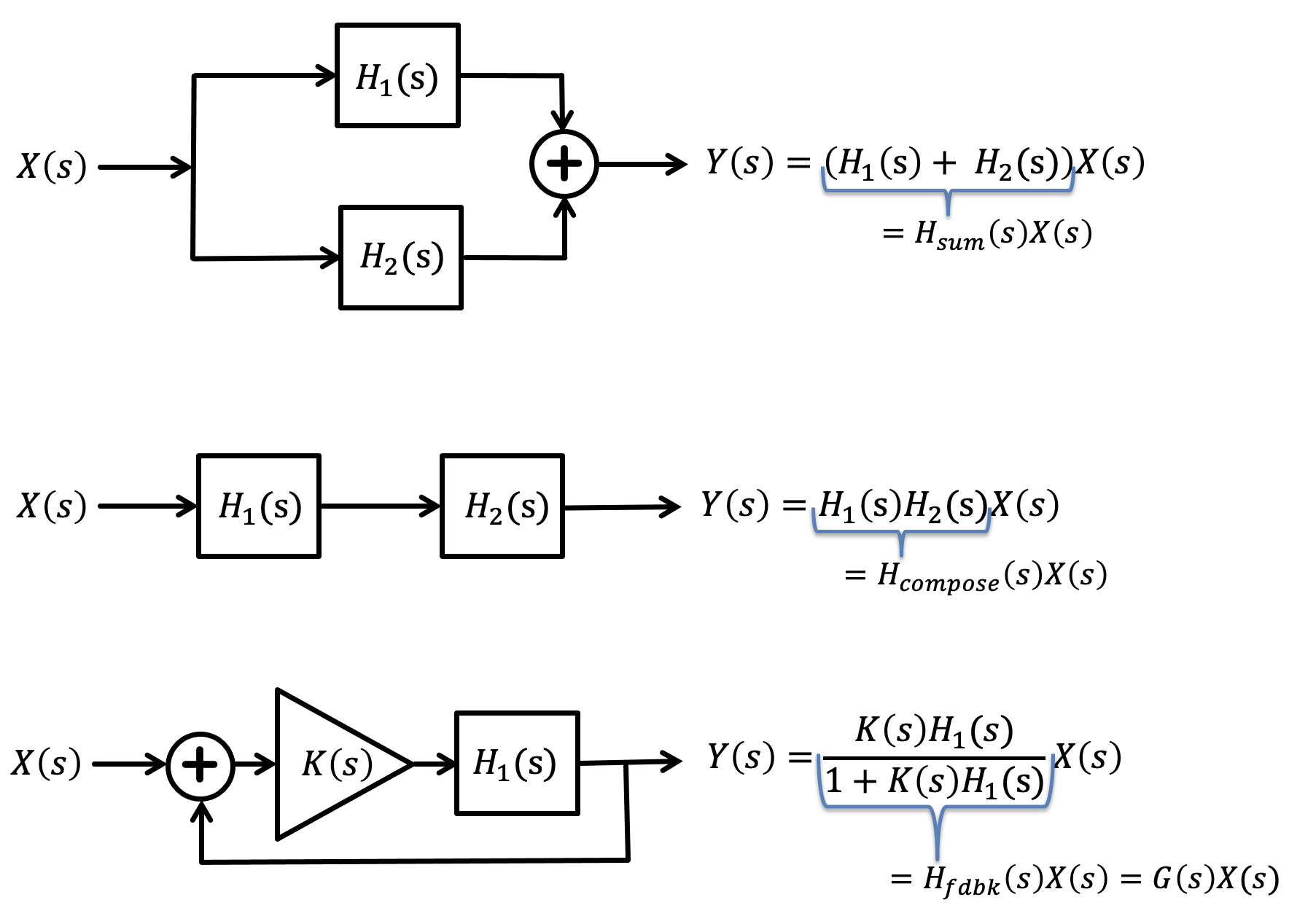
Since transfer functions are rational functions, computing products and sums is a bit more complicated that suggested by the above figure. Multiplying transfer functions involves forming products of numerator and denominator polynomials, maybe not as much fun as it sounds. Nevertheless, once you find H(s) for your composite system, you can compute poles, determine input responses, and even generate a whole-system differential equations.
Let's revist the simple model for the propeller arm, and redo it in CT. But before beginning, we note that we often prefer to write CT block diagrams and system descriptions in terms of integrals rather than derivatives. So for the propeller example, we could write the CT version of the arm equations: the time derivative of position is velocity and the time derivative of velocity is acceleration. Instead, we prefer to think of position as the time integral of velocity, and velocity the time integral of acceleration.
From the perspective of computing transfer functions, we can use either approach. Suppose, for example, that
Consider the block diagram below, showing both the time and transfer function representation of the propeller arm. In the diagram, \alpha_a(t) is the arm rotational acceleration, \omega_a(t) is the arm rotational velocity, \theta_a(t) is the arm rotation angle, \gamma is the linearized coefficent for the angle-dependent gravity-related force, \beta an air resistance coefficient, and c(t) is a command input.
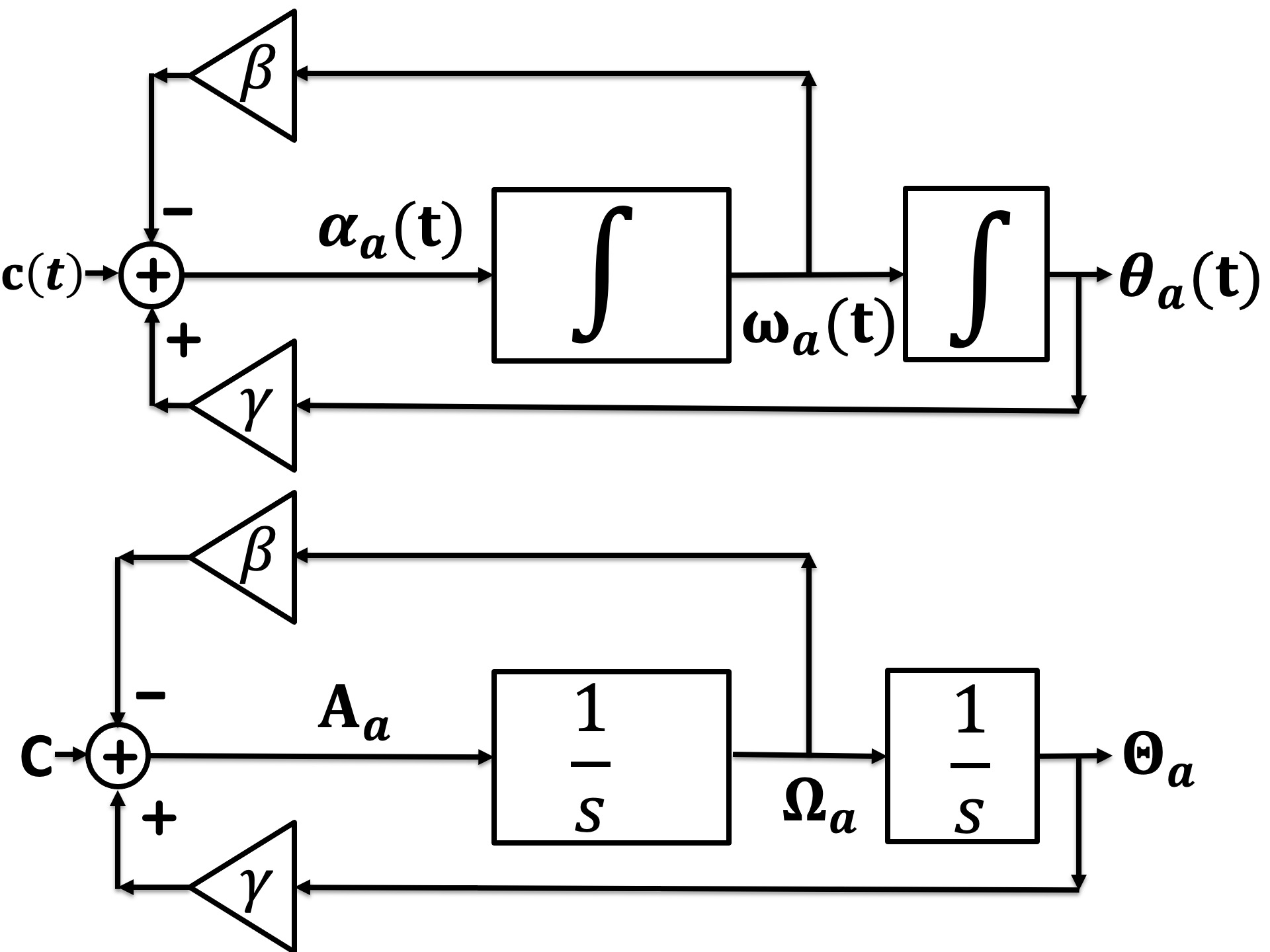
The equations for the propeller arm, using integrals and then transfer functions are:
In answering the questions below, use a python expressions. Please use B for \beta, G for \gamma and s for the s. For example, \frac{\gamma}{s^3+ \beta} should be written as 'G/(s**3 + B)'.
Give an expression for transfer function relating the input command to angle, assuming \gamma =\beta = 0,
Give an expression for transfer function relating the input command to angle, now assuming a nonzero \gamma, but \beta = 0
Give an expression for transfer function relating the input command to angle, now assuming a nonzero \beta, but \gamma = 0
Give an expression for transfer function relating the input command to angle, now assuming a nonzero \beta and nonzero \gamma
Give an expression for transfer function relating the input command to rotational velocity \Omega_a, assuming \gamma and \beta are both nonzero.
Suppose the natural frequencies of the system are 4j and -4j? What are the values of \gamma and \beta. Watch the sign of \gamma!!
Suppose the natural frequencies of the system are 2+4j and 2-4j? What are the values of \gamma and \beta.
Below are five plots of \theta(t) in response to a step change in c(t) (c(t) = 0, t < 0, c(t) = 1, t \ge 0). The five plots are numbered, and below the plots are five lettered \beta, \gamma pairs which we are asking you to match to the plots. For each of the five plots, determine the letter of the \beta, \gamma pair to make a five-letter "word" (note that "not in this list" is an option you will need, so your word should have an "N" in it!). Then give your five-letter as the answer to this question.
You should be able to solve this without resorting to computer plots. Think about the relationship between \beta, \gamma, and the pair of natural frequencies.
1: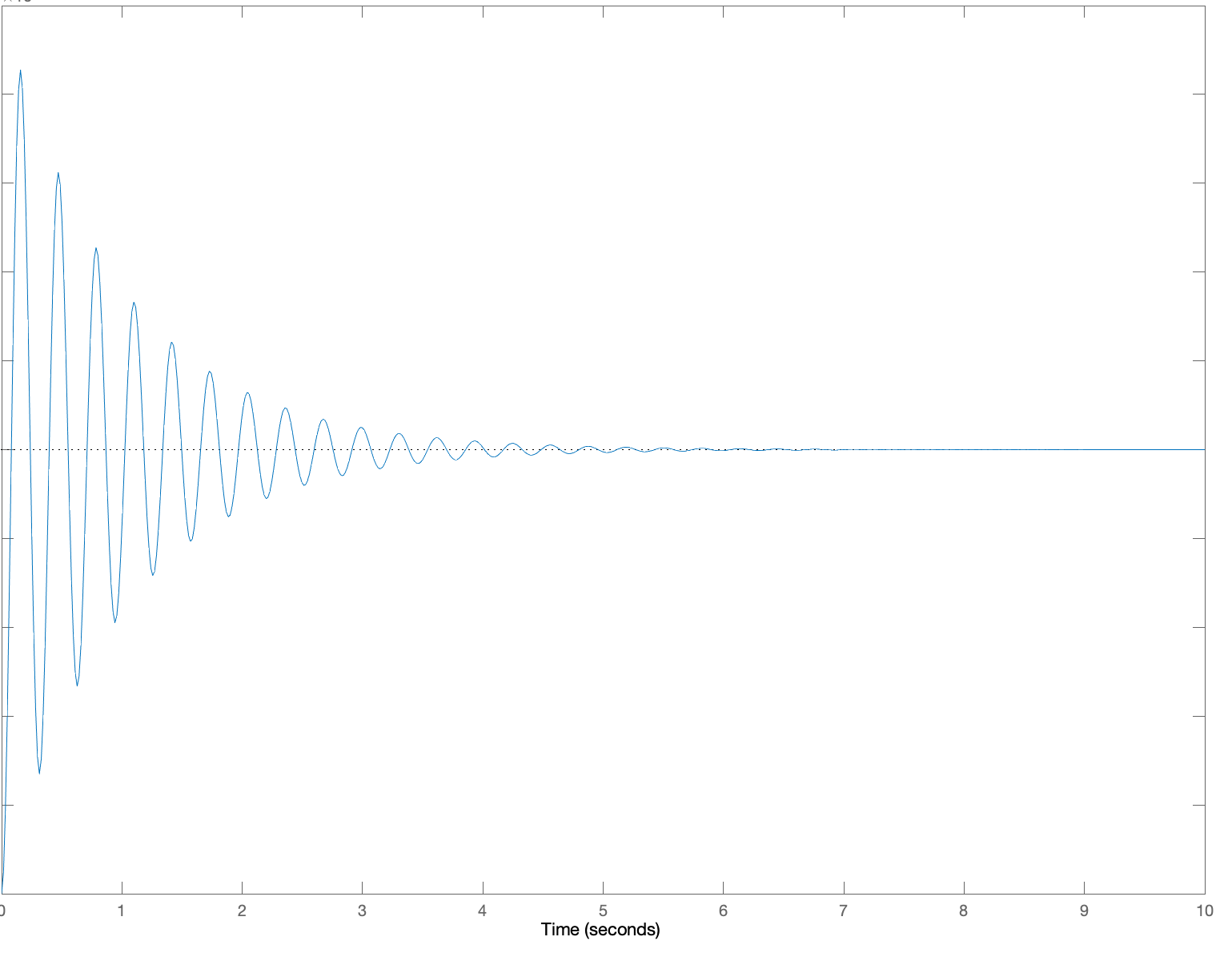
2:
3: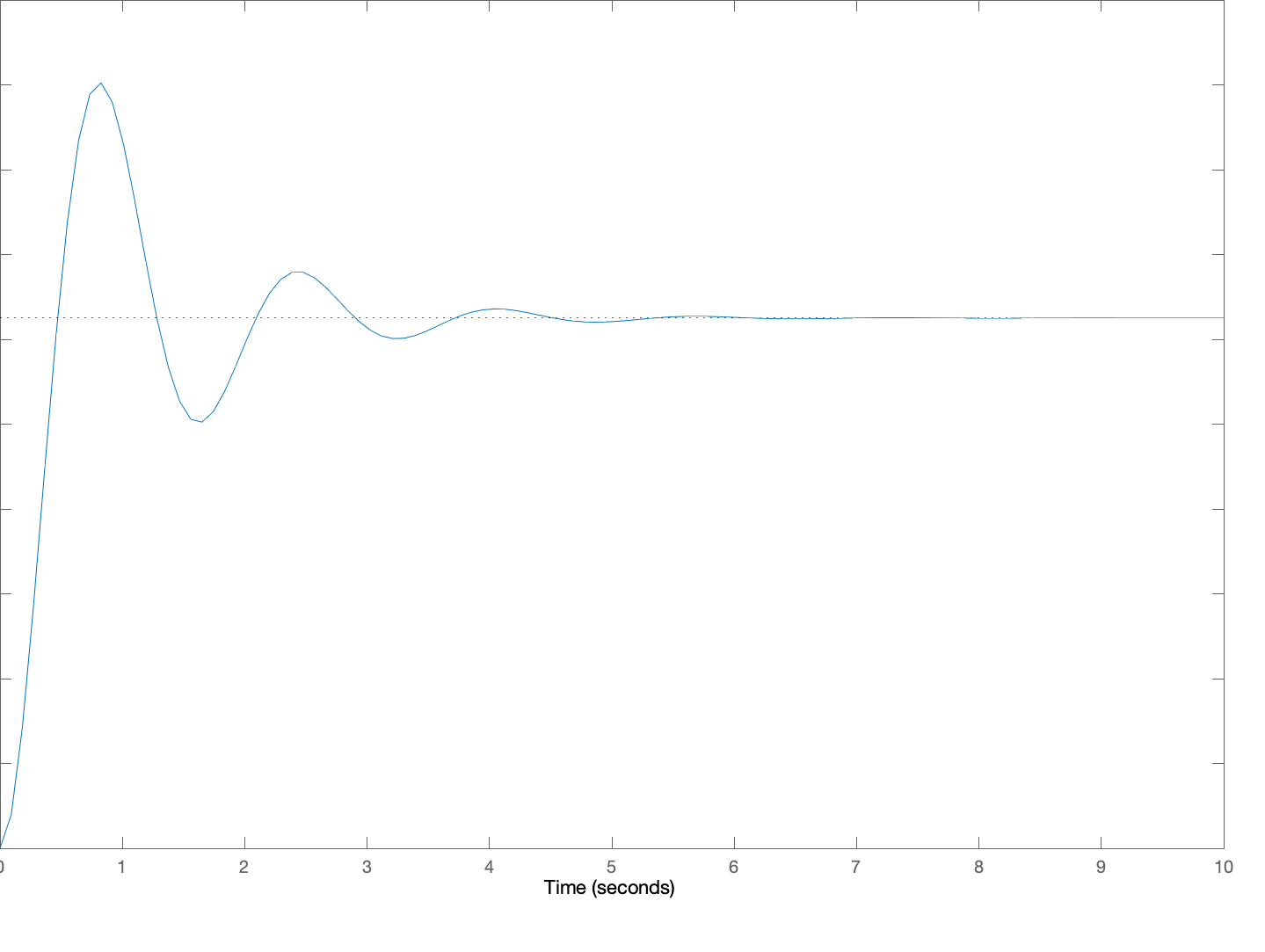
4: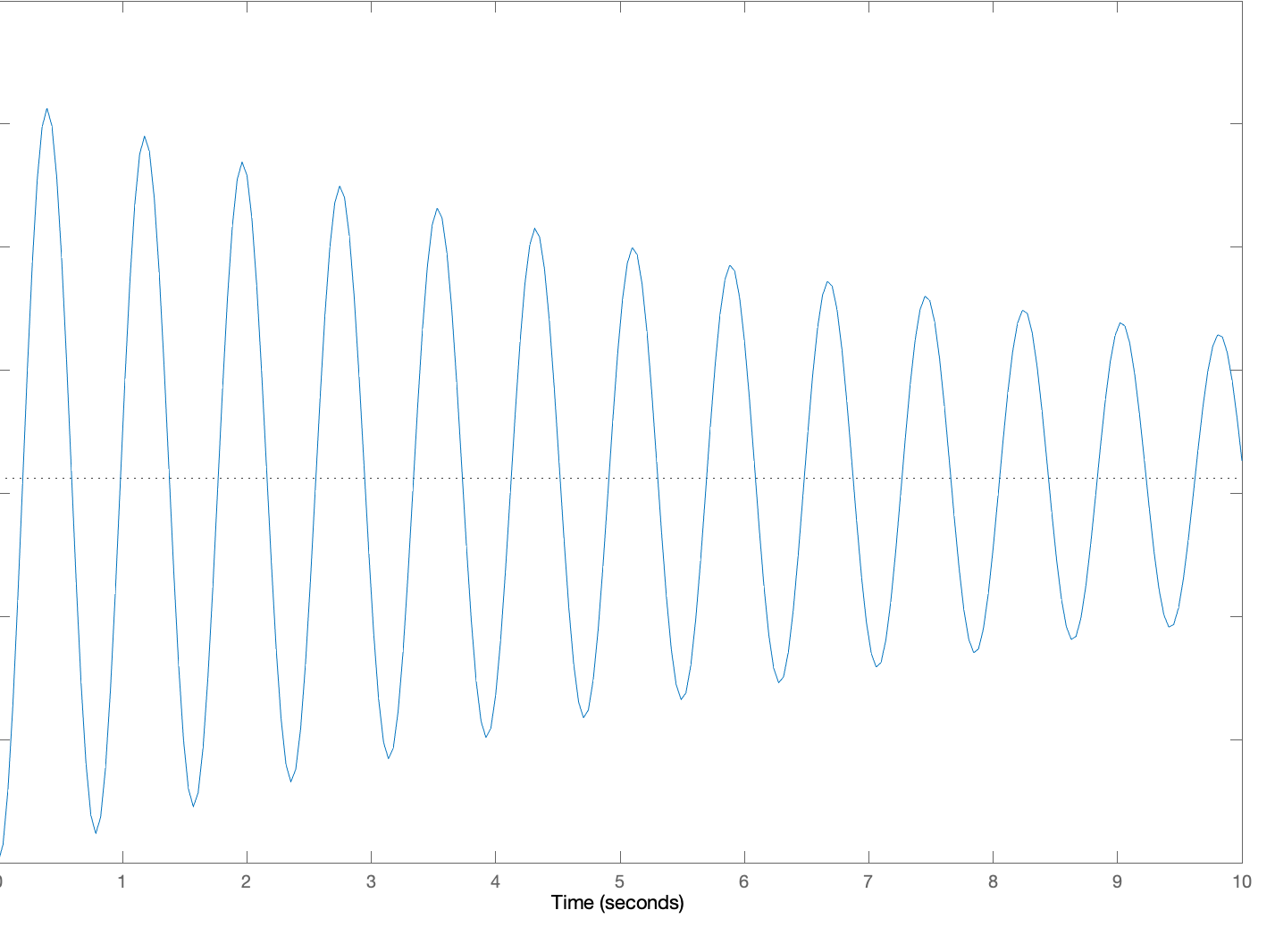
5: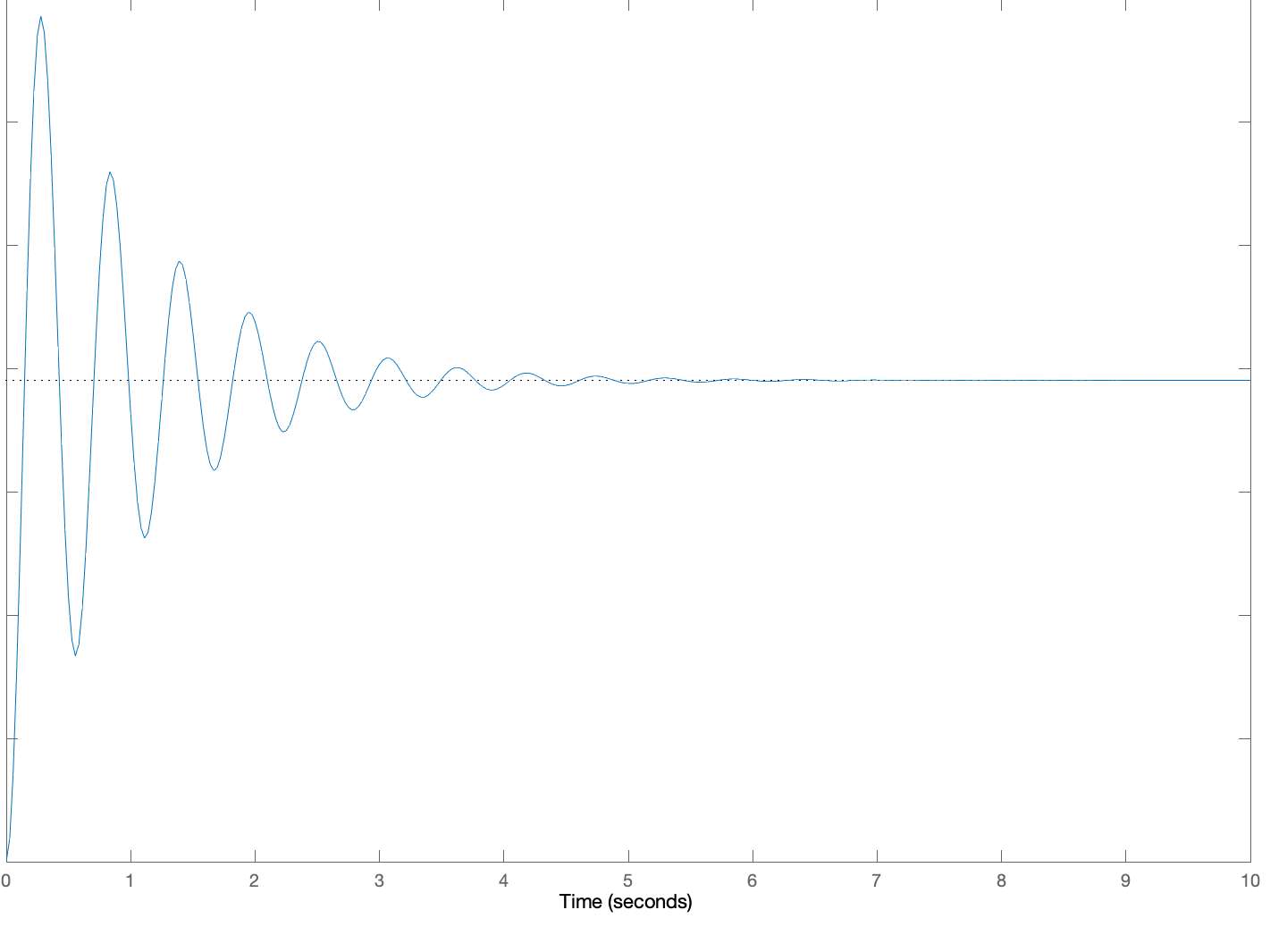
Create a five-letter "word" by matching each of the above plots to a letter associated with its \beta and \gamma pair. For example, if you think plot 1 goes with A, \beta= 0.2\;\;\ \gamma = 16, plot 2 goes with B, plot 3 with C, plot 4 with D and plot 5 is not in the list, enter 'ABCDN'. Be sure to use CAPITAL letters.
A: \beta= 0.2\;\;\ \gamma = -16
B: \beta= 0.2\;\;\ \gamma = -64
C: \beta= 2\;\;\ \gamma = -16
D: \beta= 2\;\;\ \gamma = -64
E: \beta= 2\;\;\ \gamma = -96
N: Not in this list