Thermal Example
Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.
This thermal problem makes use of the matlab script thermal.m.
As you have discovered, it can be very difficult to design a controller by first selecting candidate poles, and then using a program like place to determine the associated gains. The problem is that natural frequencies can have a complicated impact on trade-offs we care about, such as minimizing response time without exceeding equipment limits. What proved to be more effective is picking the state and input weights in a linear-quadratic regulation (LQR) scheme. In a previous postlab, we considered using LQR on a scalar discrete-time problem, mostly to gain insight into LQR. In this problem, we will try using LQR on a discrete-time system associated with temperature regulation.
A Temperature Control Example
Suppose you are designing the controller for a five-compartment heating system, as shown in the figure below. The pink compartment in the figure is the
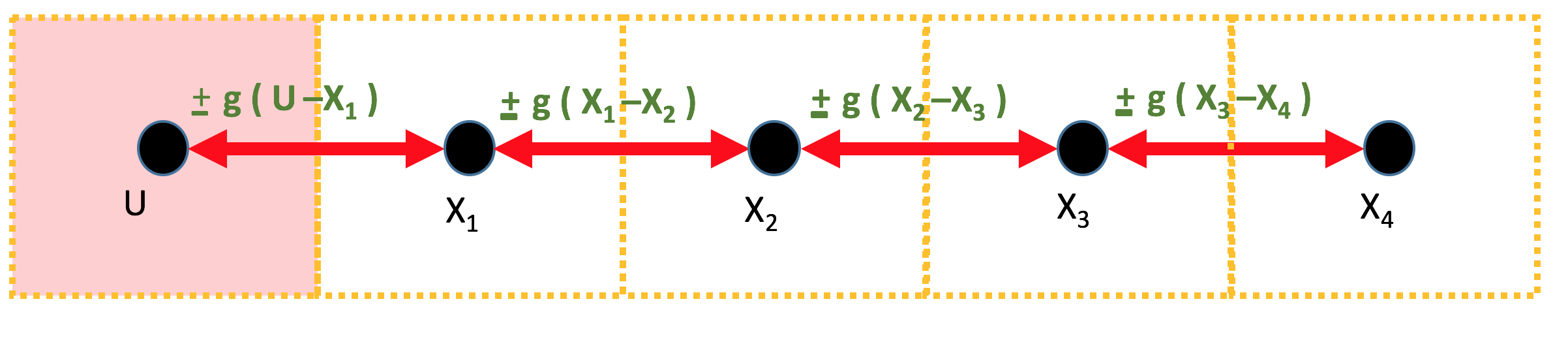
Having encapsulated the physical details in g, the equations for the temperature change in one sample period, \Delta T, are not complicated. The change is equal to the product of the period length and the difference between the "flow" in from the left, and the "flow" out to the right. That is,
Controller Design and Equipment Constraints.
For this heating system, the control problem is to adjust the heater's temperature so that all four compartments achieve a desired temperature as quickly as possible, and then adjust the heater to maintain that temperature. But, this physical system has constraints. Allowing the heater to get too hot, even briefly, is dangerous. Very high heater temperatures could start a fire, or increase the frequency and severity of accidental burns. In addition, allowing compartment temperatures to exceed the target by more than a few degrees, even temporarily, may be problematic (particularly if the compartments are occupied).
The heating system constraints should not be dismissed as a problem-specific nuisance. Every real system has physical constraints, and addressing them is a central part of control system design. If fact, we started this section with a very specific physical example, rather than equations and derivations (but those are coming too), because the constraints are easily lost in the mathematics, as is the motivation for finding a design approach other than placing natural frequencies.
Determining the Gains.
We can formulate the temperature control problem as a single-input, single-output A,B,C,D state-space system,
where \textbf{x} = [x_1,x_2,x_3,x_4]^T , u is the heater temperature, and the A,B,C,D matrices can be found in the
In the matlab script, there is a line near the top,
poles = [0.5,0.5,0.5,0.5];
which sets the desired poles, or natural frequencies, for the feedback system. These natural frequencies are used by place to determine the feedback gains,
If you try running the matlab script as is, you should see something like
the figure below. And if you examine the simulated compartment and heater
temperatures, you should notice several important characteristics. First,
the controller is fast, the compartments settle to room temperature in less
than 15 minutes. But, you should also be alarmed by how that speed was achieved.
The maximum temperatures are thousands of degrees, and the heater has
to get hotter than the surface of the sun!!. And it
may seem a little anti-climactic, but notice that temperature of the heater
also has to go negative, and refridgerate the compartments.
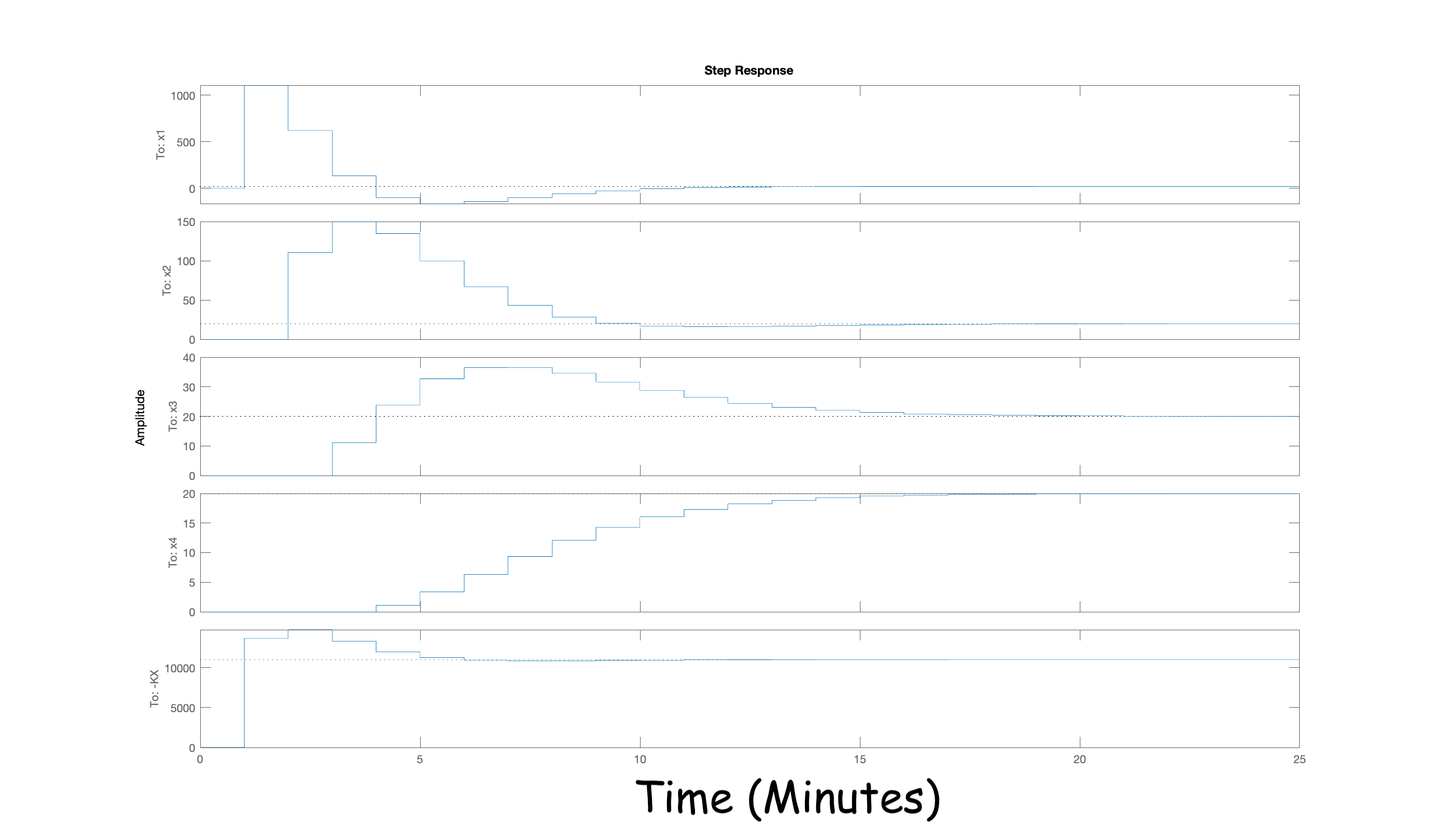
Clearly setting all the natural frequencies to 0.5 was too aggressive, but what should we do? Should we set all the natural frequencies to the same value, or should we chose several different values? And what values? In the next question, we will ask you to find natural frequency values so that place produces gains that give you controller performance that matches ours. The question is not graded, try it three times by editing the matlab script thermal.m (see the link at the top of the page), then look at our results and verify them in your code.
And before you start the next problem, please keep in mind our key point. It is very difficult to find the natural frequencies that gave a good result, Learn about LQR, another tool for determining controller gains.
You will be trying to pick natural frequencies that lead to a controller that minimizes the time for the compartments to settle to their final temperatures, while satisfying constraints associated with the physical system. The two constraints your solutions should always meet are:
- The maximum temperature of the heater must be less than 60.
- The maximum temperature in any compartment should not exceed 20.1 degrees (one tenth of a degree above the target).
Modify the natural frequency placement in the thermal.m file to set all the natural frequencies to approximately 0.99 (we have to offset them slightly for matlab's place command to work). That is, change
poles = [0.5,0.5,0.5,0.5];
to
poles = [0.99001,0.99002,0.99003,0.99004];
Can you find a set of natural frequencies that performs better than the results shown below (satisfies the constraints and settles to within one degree in less than 165 minutes)?
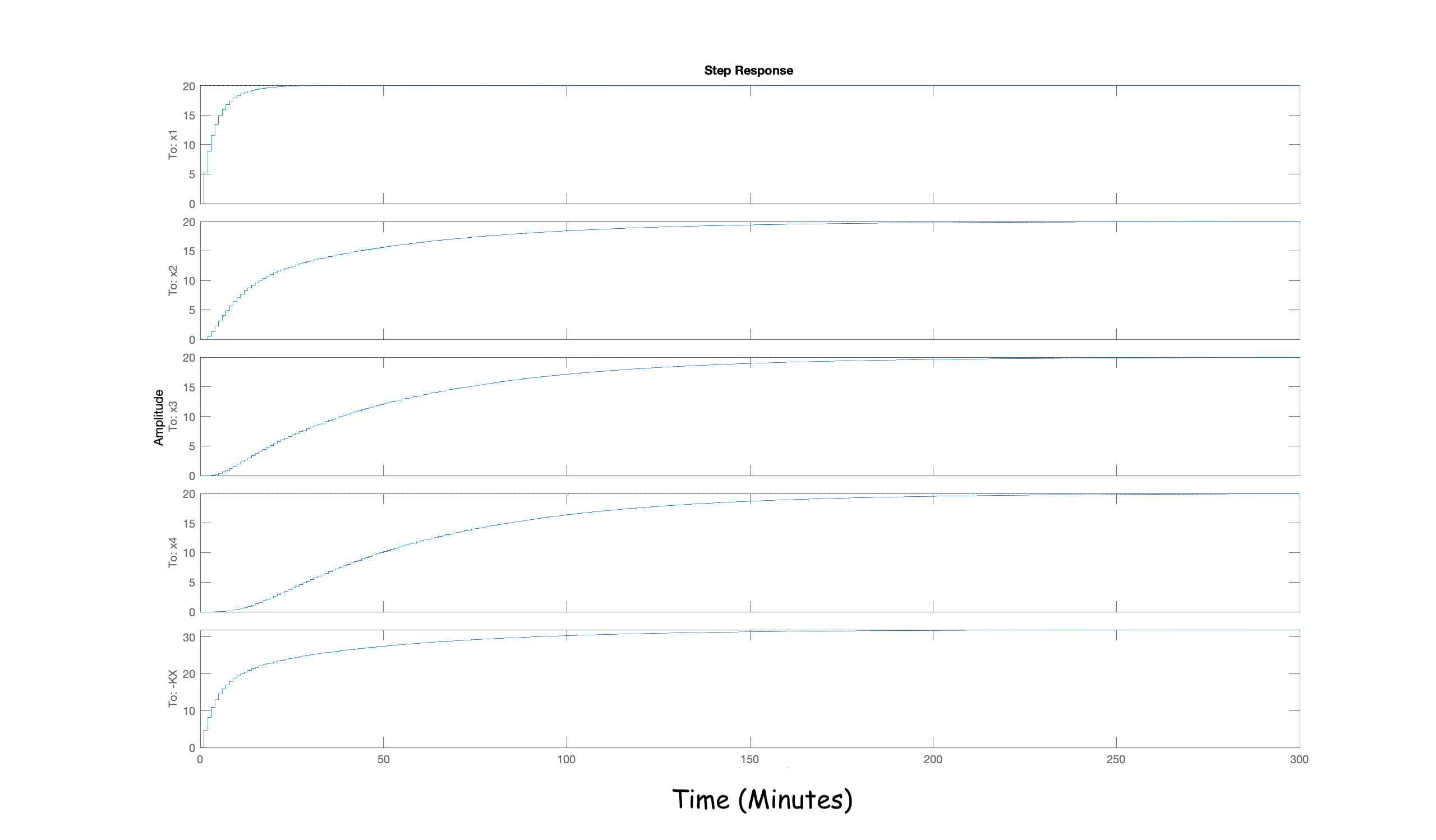
We found the following four:
[0.63,0.73,0.87,0.98]
Using OUR answer for the natural frequencies in the previous problem, and then use the matlab script to determine the associated gains for our set of natural frequencies. What were the related set of gains, to 2 digits of precision? Please note, this question is intended to help you verify that you understand the script.