Up Down Funk.

The questions below are due on Tuesday October 04, 2022; 11:59:00 PM.
 
You are not logged in.

Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.

Links for this Week

UPDATES TO BUILD AND SKETCH FOR 10/07/22!! Please check assembly guide for changes BUT IF YOU HAVE A WORKING ARM, ASK FOR HELP (we know the few steps you kneed to take to change your setup). AND DOWNLOAD THE NEW SKETCH, so you can do checkoff 4! !!!

Introduction

In the first lab, you used proportional feedback to control the propeller motor speed, which you measured using an optical encoder. In this lab, you will let your propeller-arm "fly" (well, at least rotate), and you will examine algorithms for maintaining or adjusting arm rotation by adjusting the propeller-generated thrust. More specifically, you will use an ad-hoc approach to designing a proportional-delta (PD) controller, then examine your controlled system's responses, extract natural frequencies, and use them to calibrate a second-order difference equation model of the arm. Then you will use your model to determine how the controlled-system's natural frequencies will change as a function of proportional and delta controller gains, and use that insight to design a better controller. And you will succeed, sort of. By the end of the lab, you should have an okay controller, but should be pretty dissatisfied with the match between experiment and model.

Determining more complete models and designing more sophisticated control strategies requires an approach to analyzing systems that offers more insight than just writing down parameterized systems of difference equations and computing their natural frequencies. Starting next week, we begin developing the mathematical tools for generating more complicated models by composing small blocks, using approaches that also provide insight into how the smaller blocks impact the larger system.

Summary of Lab Tasks

There are four checkoffs in this lab, all of which can be done with partners. For the first checkoff, you need only demonstrate your working arm and your understanding of its behavior without adding proportional (K_p) or delta/derivative (K_d) feedback. For the second checkoff, you will be using proportional feedback alone, and comparing the natural frequencies of a difference equation model of your arm with its measured behavior, to extract \gamma. Using the model parameter (\gamma) you determined in checkoff two, you will investigate the properties of the arm when using proportional plus derivative control, develop an intuition about the influence of the delta/derivative feedback, and compare the model predictions with what happens on the arm. Finally, in check-off 4, you will look at the behavior of the system when the inputs are sinusoids.

Summary of Setup Tasks (Checkoff 1).

  • Download the sketch for this lab, 6310_PROP_22_WS.zip.
  • On the Resources drop-down menu, click on the "Propeller Arm Assembly Guide" and assemble and test the arm control hardware using parts from your kit plus five new three-d printed parts (linker, angle sensor bracket, 2-sided arm holder, and two dual-Large-motor brackets). New parts are on lab table.

Calibration and Correction

As noted in the assembly guide, you should calibrate the angle sensor, and adjust the propeller drive so that the thrust is pushing the arm upward.

Computing dThetaErr/dT

An approximation for the derivative of the angle error is given by the difference equation

dThetaErrDt[n] = \frac{e[n]- e[n-mBack]}{mBack \Delta T}
where m is the number of points back. If m is large, the "derivative" is less noisy, but is less "up to date". If m is small, the "derivative" is noisy, but is also more immediate.

Block Diagram for Computing the Scaled Delta.

Analysis software

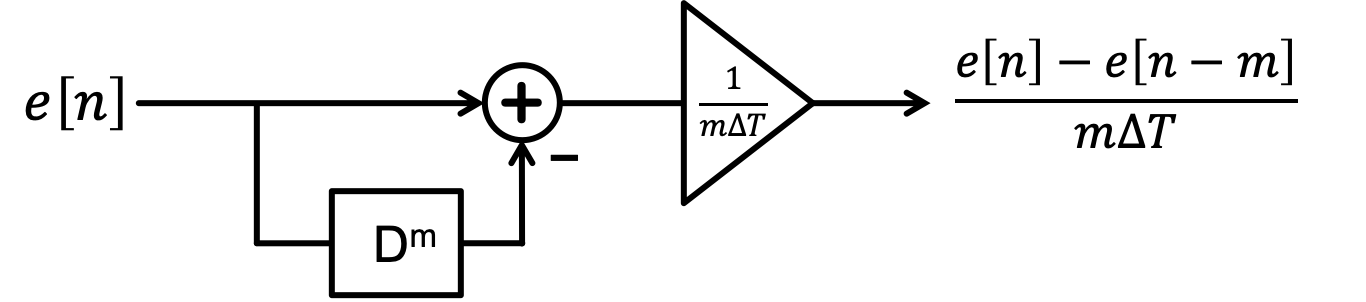
Today we will use python to determine natural frequencies by finding the roots of polynomials associated with higher order difference equations. You may also find it helpful to plot those roots as a function of controller gain parameters (the so-called "root locus").

Checkoff One: Testing and Open-Loop Arm Positioning.

In the prelab, you examined this rotating arm case, with the thrust set by adjusting the equivalent of a nominal command in this lab, but WITHOUT adjusting the thrust based on arm-angle feedback (updown funk prelab question) (Kp=0 and Kd=0). You analyzed +45^{\circ} angle (above horizontal) and -45^{\circ} angle (below horizontal), which was stable?

UPDATES TO BUILD AND SKETCH FOR 10/07/22!! Please check assembly guide for changes BUT IF YOU HAVE A WORKING ARM, ASK FOR HELP (we know the few steps you kneed to take to change your setup). AND DOWNLOAD THE NEW SKETCH, so you can do checkoff 4! !!!

Checkoff 1:
  • What does the parameter "plotIncrement" at the top of the sketch do?
  • What does setting "PLOTALL" to one at the top of the sketch do?
  • What was different about the +45^{\circ} angle (above horizontal) and -45^{\circ} angle (below horizontal)?

Building Up Our Model

Variable Table and Control Diagram.

  • l: Arm length (\text{m})
  • m: Propeller mass
  • a_A: linear acceleration of the end of the arm
  • f_A: net force acting at the end of the arm
  • f_a = f_A - f_0: perturbation from gravity-balancing thrust needed to hold \theta_0 (horizontal arm in our case).
  • c: perturbation from motor command that force-balances at \theta_0.
  • \alpha_a: Arm angular acceleration (\text{rad}\cdot s^{-2})
  • \omega_a: Arm angular velocity (\text{rad}\cdot s^{-1})
  • \theta_A is the measured arm angle (in \text{radian}).
  • \theta_a = \theta_A - \theta_0, the measured perturbation from \theta_0. (\text{radians}).
  • \theta_d: Desired perturbation from \theta_0 (\text{radians}).
Overall System Feedback Diagram::

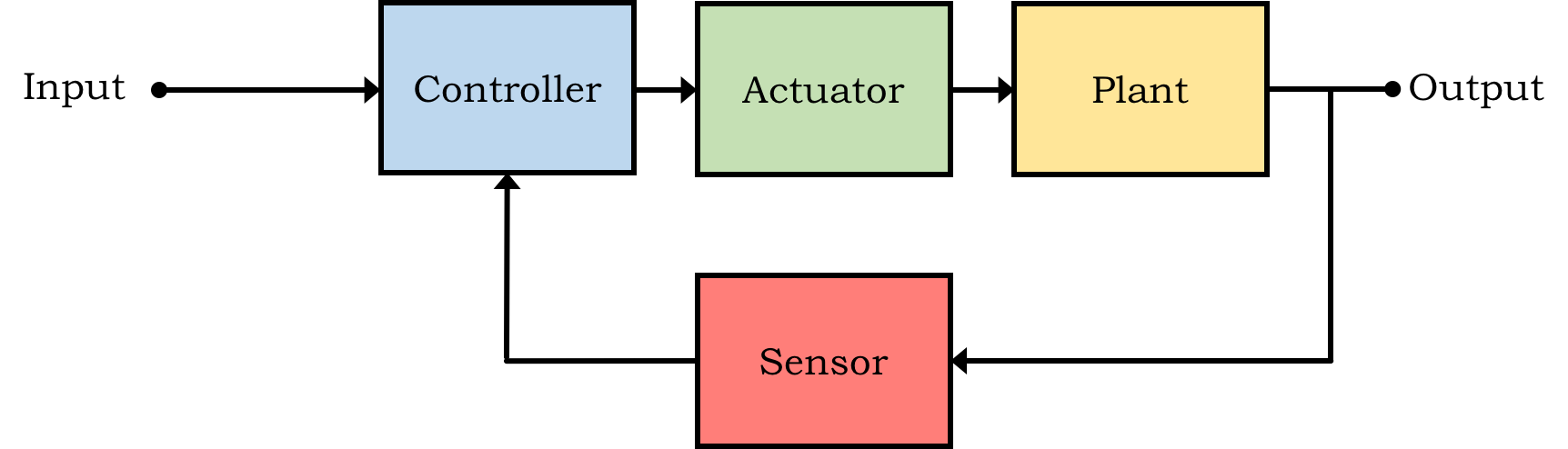
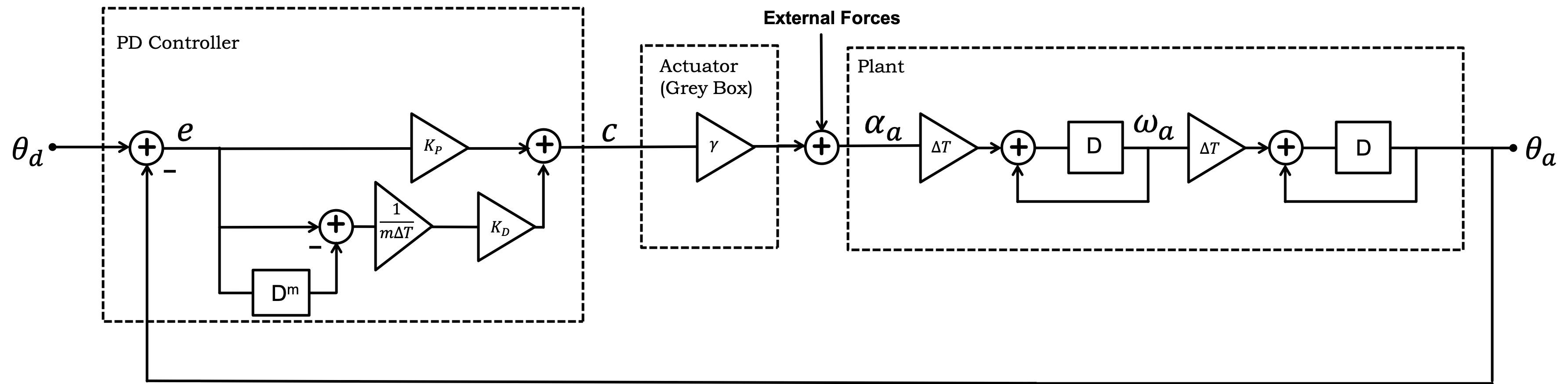
Just like in Lab 1 where we had a controller for our motor velocity, in this lab we have a controller for our angle. Most feedback systems can be thought of in general as shown in the image above. As a review/refresher, let's first go through derivations for each of the four major feedback blocks

Modeling the Acceleration

The plant model is an input-output model derived from the physics of the system we are trying to control, and in this case is a model of the copter-levitated arm. The input is the voltage across the propeller motor wires, the output is the arm angle sensor, a magnepot. The propeller-plus-motor is sometimes referred to as an actuator (as it moves the arm by generating thrust), and the magnepot (the small black part that looks like a potentiometer) is clearly the sensor (because it measures \theta_A.)

Because the chopstick is light, the forces on the arm are (approximately) applied to the tip of the arm where the propeller is located. The forces include the propeller generated thrust, the force due to gravity and any wind resistance when the arm is rotating. We denote this net force as f_A, and accelerates the tip of the arm, a_A = \frac{f_A}{m}, as shown in the figure below.

Acceleration:: A force is applied to the end of the propeller arm, which is transformed into a "pivoted" linear acceleration, which is itself responsible for an angular acceleration $\ddot{\theta_A} = \ddot{\theta_a} = \alpha_a.$

Turning this into equations that we have been getting used to in this class we could also say:

f_A[n] = m \; a_A[n]
or
a_A[n] = \frac{f_A[n]}{m}

That linear acceleration at the location of the propeller will result in motion of the arm pivoted around the axis of rotation (our angle sensor). Equivalently, the angular acceleration of the arm, \alpha_A, is given by

\alpha_A = \frac{a_A}{l}
where l is the length of the arm. Again we can turn this into a discrete time expression like so:
\alpha_A[n] = \frac{a_A[n]}{l}
or with f_A[n] involved it would be:
\alpha_A[n] = \frac{f_A[n]}{ml}.

Just like linear acceleration, if angular acceleration is the constant \alpha_a[n-1] for the time between the n-1 and the n, then the change in angular velocity, \omega_a, is given by

\omega_a[n] = \omega_a[n-1] + \Delta T \cdot\alpha_a[n-1],
where \Delta T is the duration of our timestep in seconds. Note here than we have switched to \alpha_a = \alpha_A - \alpha_0 and \omega_a = \omega_A - \omega_0, because \alpha_0 = 0 and \omega_0 =0. That is, we linearized about a force-balanced steady-state where the motion was zero.

Getting the Angle

We just showed that we can generate an angular velocity from angular acceleration using a discrete time integrator. Since angle is based on the integral of velocity can we do this again to figure out the angle? Yes, we can. It'll look like the following.

\theta_a[n] = \theta_a[n-1] + \Delta T \cdot \omega_a[n-1]
where we have used the fact the \theta_a = \theta_A - \theta_0 and that \omega_0 is zero (we linearized about a force-balanced steady-state), so \omega_A = \omega_a.

When drawn in block diagram form, we get the following picture:

Angle from Angular Velocity:

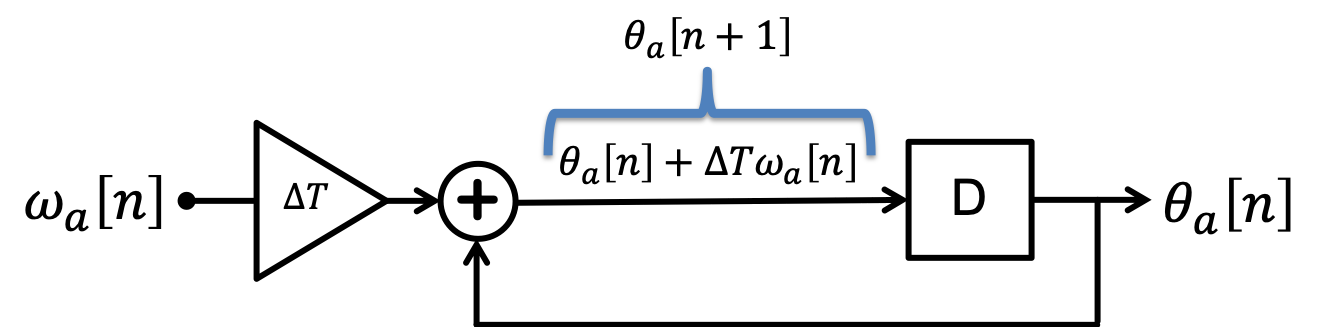
Again we see a discrete time integrator in place.

The Plant Overall Let's put everything we just did together into one giant block diagram. Note we put the mass, arm-length scaling term out from as well so that the input to this plant overall is f_a. The blocks we've already covered are in series resulting in the following overall plant:

Angle from force:

The Actuator

In our system, the actuator is the propeller, which takes a motor command c and generates a thrust f_a. For this lab, we are making the approximation that the thrust from the propeller changes instantly after a change in motor command, with a scale factor we denote as b. But that means we are ignoring exactly the dynamic we investigated in the speed control lab. That is, the thrust is related to how fast the propeller spins, and the propeller rotation speed does not change instantly after a change in motor command. Look for inconsistencies between model and physical behavior!

We can combine unknown parameters in the model, the motor command to thrust relation, c \rightarrow f_a, and the thrust to rotational acceleration relation, f_a \rightarrow \alpha_a, into a "grey-box" model which will consist of just a term \gamma. As in,

\alpha_a[n] = \frac{b}{m\cdot l}c[n] = \gamma c[n].

Proportional Control

When we set the nominal command so that the copter hovers at horizontal, we are determining the nominal motor command that creates exactly the thrust needed to balance gravity (for the horizontal arm) so we can assume they cancel when analyzing the controller.

By proportional control, we mean that

c[n] = K_p\left(\theta_d[n]-\theta_a[n]\right)
where c[n] is the perturbation from the forcing-balancing-at-horizontal nominal command to the motor, K_p is our proportional gain, \theta_d[n] is our desired perturbation in arm angle, and \theta_a[n] is our measured perturbation in arm angle. When we set the nominal command so that the copter hovers at horizontal, our direct term is creating exactly the thrust needed to balance gravity, so we can ignore them when analyzing the controller.

For the case of proportional feedback control, the system diagram is as shown below.

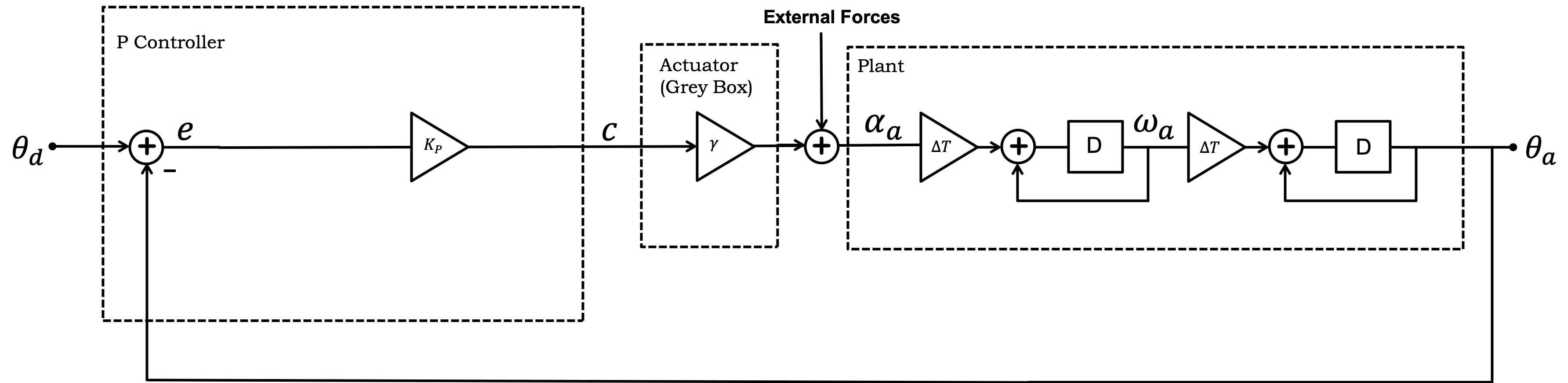
Proportional Feedback:Overall system diagram for proportional feedback

Test the proportional controller:

  • Set a small value of Kp (type "3 0.1" in the send window of the plotter).
  • Set the nominal command (adjust the potentiometer) so the arm hovers at about horizontal.
  • Tap the copter arm or blow on the propeller and gauge how far the arm is disturbed.
  • Increase the proportional gain (while holding the arm horizontal) and then tap the arm. You should be ready to stop your propeller from going crazy! See if you can generate slowly grow oscillations with different periods, and use the result to estimate \gamma.

Determine an analytic formula for the natural frequencies of the difference equation describing the proportional feedback system above as a function of \gamma and K_p. What can you say about the stability of the system?

Check Yourself 1:

To have a stable system, where must the natural frequencies be on the complex plane?

UPDATES TO BUILD AND SKETCH FOR 10/07/22!! Please check assembly guide for changes BUT IF YOU HAVE A WORKING ARM, ASK FOR HELP (we know the few steps you kneed to take to change your setup). AND DOWNLOAD THE NEW SKETCH, so you can do checkoff 4! !!!

Checkoff 2:
  • Show a staff member the operation of the copter arm under just P control, demonstrating the oscillation frequency.
  • Show your difference equation, your formulas for the natural frequencies, and plots of the natural frequency versus proportional gain.
  • What does the theory predict about the stability of the P controlled system?
  • How do your predictions compare to your experimental results?

PD Control

To stabilize the system we are going to add deltaErr/dT term to proportional feedback. Since the delta in error is scaled by \Delta T, this is sometimes considered an approximation to derivative feedback.

PD Controller and System Diagram:

The difference equation for the motor command is given by

c[n] = K_p\left(\theta_d[n] - \theta_a[n]\right) + K_d\left(\frac{\theta_d[n] - \theta_a[n] - \theta_d[n-mBack] +\theta_a[n-mBack]}{mBack \Delta T}\right).

The difference equation relating \theta_d[n] to \theta_a[n] is a bit complicated to derive, so we give it below.

\theta_a[n] -2\theta_a[n-1] + \theta_a[n-2]\left(1+\gamma K_p\Delta T^2 + \gamma K_d \frac{\Delta T}{mBack}\right) -\theta_a[n-2-mBack]\gamma K_d \frac{\Delta T}{mBack}
= \theta_d[n-2]\left(\gamma K_p\Delta T^2 + \gamma K_d \frac{\Delta T}{mBack}\right) -\theta_d[n-2-mBack]\gamma K_d \frac{\Delta T}{mBack}.

How many natural frequencies are there for the LDE that describes PD feedback for mBack=3?

How many natural frequencies are there for the LDE that describes PD feedback for mBack=5?

Experiment

In this last experiment, we would like you to explore the PD controller design space. You have several parameters to play with, K_p, K_d and m. You can set K_p and K_d from the serial plotter send window. For example, type 3 2.3 to set K_p to 2.3, and 4 0.2 to set K_d to 0.2. Try starting with mBack=3 (, and test with K_p = 0.5,1,5, 10. For each K_p, what value of K_d gives the most stable arm (when you disturb it by tapping)? Try toggling small desired angles (thetahigh and thetaLow at the top of the sketch to +/-0.1) and then larger angles (+/-0.4). How do your results relate to the natural frequencies for the difference equation model? Note that for mBack=1 and higher, the difference equation model is 3rd order or higher, so you will need a computational root finder (you can use our python program at the top of this lab) to determine the natural frequencies. What conclusions do you draw about how well the difference equation is matched to the propeller problem? You predicted a \gamma in checkoff 2, could you reextract a better \gamma, one that would be more predictive?

After you have decided on a good set of values, try the following:

  • Set K_d and K_p to the best values you calculated based on your experiments and the difference equation model (use the attached python program to make and show plots).
  • Tap the arm and look at the disturbance response.
  • Set your toggle values (at the top of the sketch) to +/-0.1,
  • Do you notice any asymmetries between positive steps and negative steps?
  • You probably saw that too much K_d caused noise and vibrations to dominate, does making m larger than three help? How does the maximum usable value of K_d change as m is increased? What limits the usable range of m?

UPDATES TO BUILD AND SKETCH FOR 10/07/22!! Please check assembly guide for changes BUT IF YOU HAVE A WORKING ARM, ASK FOR HELP (we know the few steps you kneed to take to change your setup). AND DOWNLOAD THE NEW SKETCH, so you can do checkoff 4! !!!

Checkoff 3:
  • What do the natural frequencies of the difference equation model tell you about the impact of adding delta/derivate feedback?
  • How do the natural frequencies of the difference equation model relate to your observed step responses?
  • How does the motor command behavior change as Kd increased?
  • If you set K_d so that \frac{K_p}{K_d} \approx 4, and then allow K_p to vary from one to ten (so K_d varies from 0.25 to 2.5), how does the propeller system behavior relate the natural frequencies of the difference equation model?
  • What was the result of increasing mBack in the Teensy code?
  • How did you pick a "best" set of parameters?
  • If you set Kp=10, can you adjust mBack and Kd to get good results?
  • Do you see effects that are inconsistent with your model?

If we input a sinusoid into a system described by linear differential or difference equations, and if the system is stable, then the output will eventually settle to a sinusoid of the SAME frequency, but NOT THE SAME AMPLITUDE and PHASE (we will clarify phase later). We refer to the settled sinusoid response as the sinusoidal steady state, and refer the relationship between the frequency of a sinusoidal input to the amplitude and phase of the system's sinusoidal steady-state output as the system's FREQUENCY RESPONSE. Clearly frequency responses can only be measured for systems that are stable, because unstable systems will not settle to a sinusoidal steady state, and the propeller arm without feedback is NOT STABLE! We know we can stabilize the arm with a PD controller, but as you will see below, the controller will affect the frequency response we measure. In the next lab, we will investigate frequency response in more detail, but for now, just keep in mind that we will need a de-embedding process if we want to using the frequency response of the propeller-arm with feedback control to determine the innate frequency response of the propeller-arm system.

But, we are getting ahead of ourselves. Above, you applied a PD-controller, and investigated the relationship between different PD controllers and the amount of ringing in their step responses. Now, we are going to have you examine, just experimentally, the impact of a PD controller on the response to sinusoids of different frequencies.

First, try this! In your sketch, make sure highTheta is set to 0.15, lowTheta is set to -0.15 and mBack is set to 5. In the serial plotter send window, set reasonable values for K_p (e.g. type "3 2.0") and K_d (e.g. type "4 0.5"), and then set the input to a sinusoid with frequency 0.5 by typing "5 0.5". You should see a sine wave being plotted (you can switch by to square waves by typing "5 0").

Steps:
  1. Set the values of Kp, Kd, and sinusoid frequency (parameters 3, 4, and 5 respectively when setting using the serial plotter), and examine step and sinusoid responses.
  2. Determine QUALITATIVELY the relationship between the Kp/Kd ratio, ringing in the step response, and peaking in the frequency response.

Checkoff 4:

  • Set K_p = 2 and set K_d to give you a step response with no overshoot. Then pick 10 frequency points in the range of 0.5 -> 3, and plot the ratio of the input to output sinusoid amplitudes versus frequency. What trends do you see?

  • Set K_p = 2 and set K_d to give you a step response that overshoots and oscillates before settling down. Then pick 10 frequency points in the range of 0.5 -> 3, and plot the ratio of the input to output sinusoid amplitudes versus frequency. What trends do you see?

  • Try switching directly from a low frequency (e.g. 0.5) and the frequency that produces the large amplitude output (maybe 1.8?). How long does the response take to settle?