PD Controller with Disturbances.
Please Log In for full access to the web site.
Note that this link will take you to an external site (https://shimmer.mit.edu) to authenticate, and then you will be redirected back to this page.
Consider the following block diagrams, in the discrete-time and z, for an alternative model of the relation between rotational velocity and rotation angle.
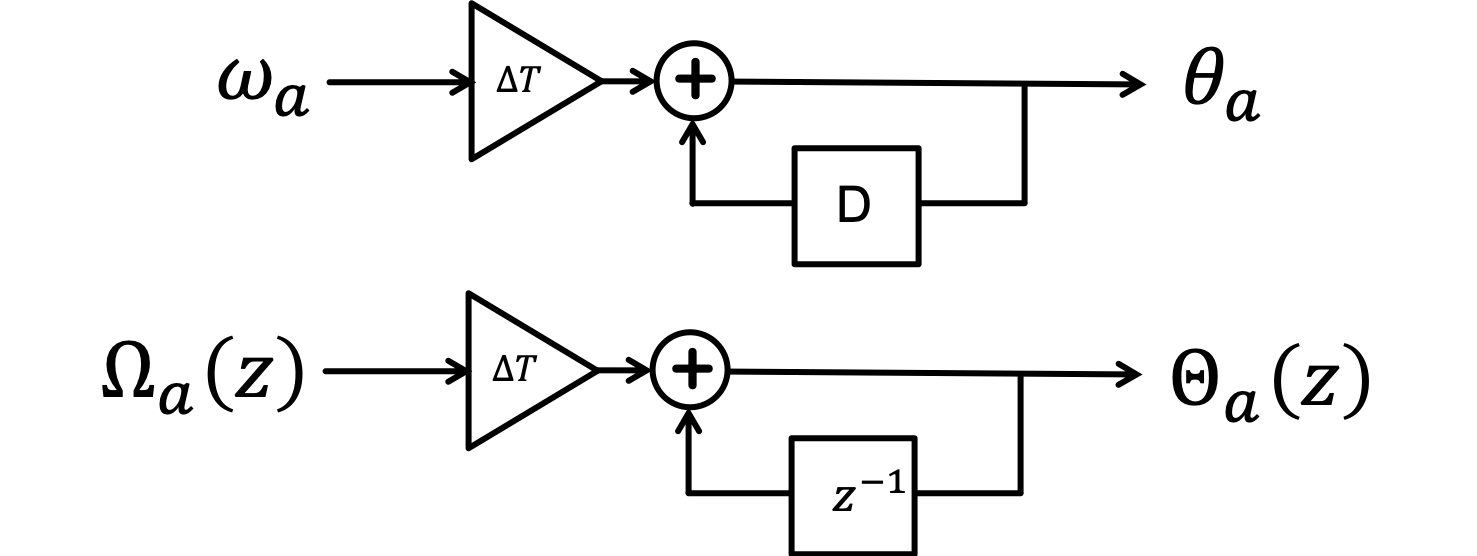
Based on the above diagram, which of the following difference equations relates the sequence \omega_a to the sequence \theta_a?
Equation I: \theta_a[n] = \theta_a[n-1] + \Delta T \omega_a[n-1],
Equation II: \theta_a[n] = \theta_a[n-1] + \Delta T \omega_a[n],
Equation III: \theta_a[n] = \theta_a[n] + \Delta T \omega_a[n],
Based on the above diagram, which \mathcal{H}(z) (transfer function), I,II, or III, satisfies \Theta_a(z) = \mathcal{H}(z) \Omega_a(z) ?
Equation I: \mathcal{H}(z) = \frac{\Delta T}{1 - z^{-1}} ,
Equation II: \mathcal{H}(z) = \frac{\Delta T z^{-1}}{1 - z^{-1}} ,
Equation III: \mathcal{H}(z) = \Delta T (1 - z^{-1}),
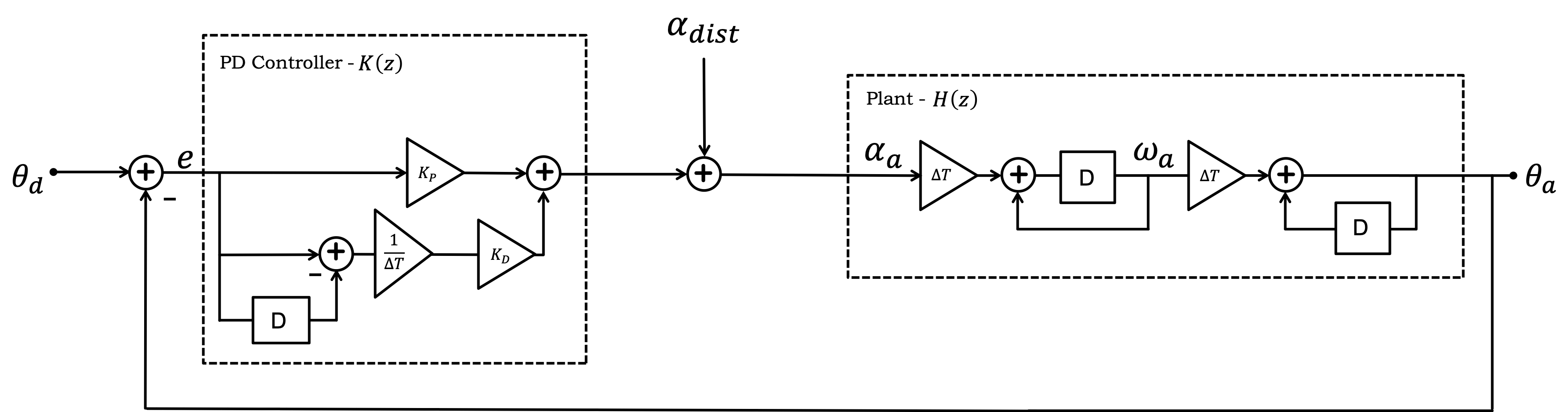
From the above block diagram, we have the familiar transfer functions for the controller,
We can write the closed-loop transfer functions from desired input, \Theta_d(z), and from disturbance, \Alpha_{dist}(z), to the output, \Theta_a(z), in the form
We can relate the two transfer closed-loop transfer functions, \mathcal{G}(z) and \mathcal{G}_{dist}(z) to \mathcal{K}(z) and \mathcal{H}(z), using variants of Black's formula. Which of the following statements is correct?
Statement I: \mathcal{G}_{dist}(z) = \frac{\mathcal{K}(z)}{1+\mathcal{K}(z) \mathcal{H}(z)} and \mathcal{G}(z) = \frac{\mathcal{K}(z)\mathcal{H}(z)}{1+\mathcal{K}(z)\mathcal{H}(z)}
Statement II: \mathcal{G}_{dist}(z) = \frac{\mathcal{H}(z)}{1+\mathcal{K}(z) \mathcal{H}(z)} and \mathcal{G}(z) = \frac{\mathcal{K}(z) \mathcal{H}(z)}{1+\mathcal{K}(z)\mathcal{H}(z)}
Statement III: \mathcal{G}_{dist}(z) = \frac{\mathcal{K}(z) \mathcal{H}(z)}{1+\mathcal{K}(z) \mathcal{H}(z)} and \mathcal{G}(z) = \frac{\mathcal{H}(z)}{1+\mathcal{K}(z)\mathcal{H}(z)}
From the above diagram, one can determine the transfer closed-loop transfer functions as rational functions in z. Be careful to note that the plant is a mixture of the alternative model above and the more typical model, and determine the closed-loop transfer functions in the forms,
The coefficients A_1, A_2, B_1, B_2, Bd_1 and Bd_2 are all functions of K_d, K_p, and \Delta T. Below please give the expressions for each using python syntax and use dt for \Delta T, Kp for K_p, and Kd for K_d. For example, to enter \frac{K_d}{\Delta T}, type Kd/dt, to enter -(1 + 2 K_p), type -(1+2*Kp).
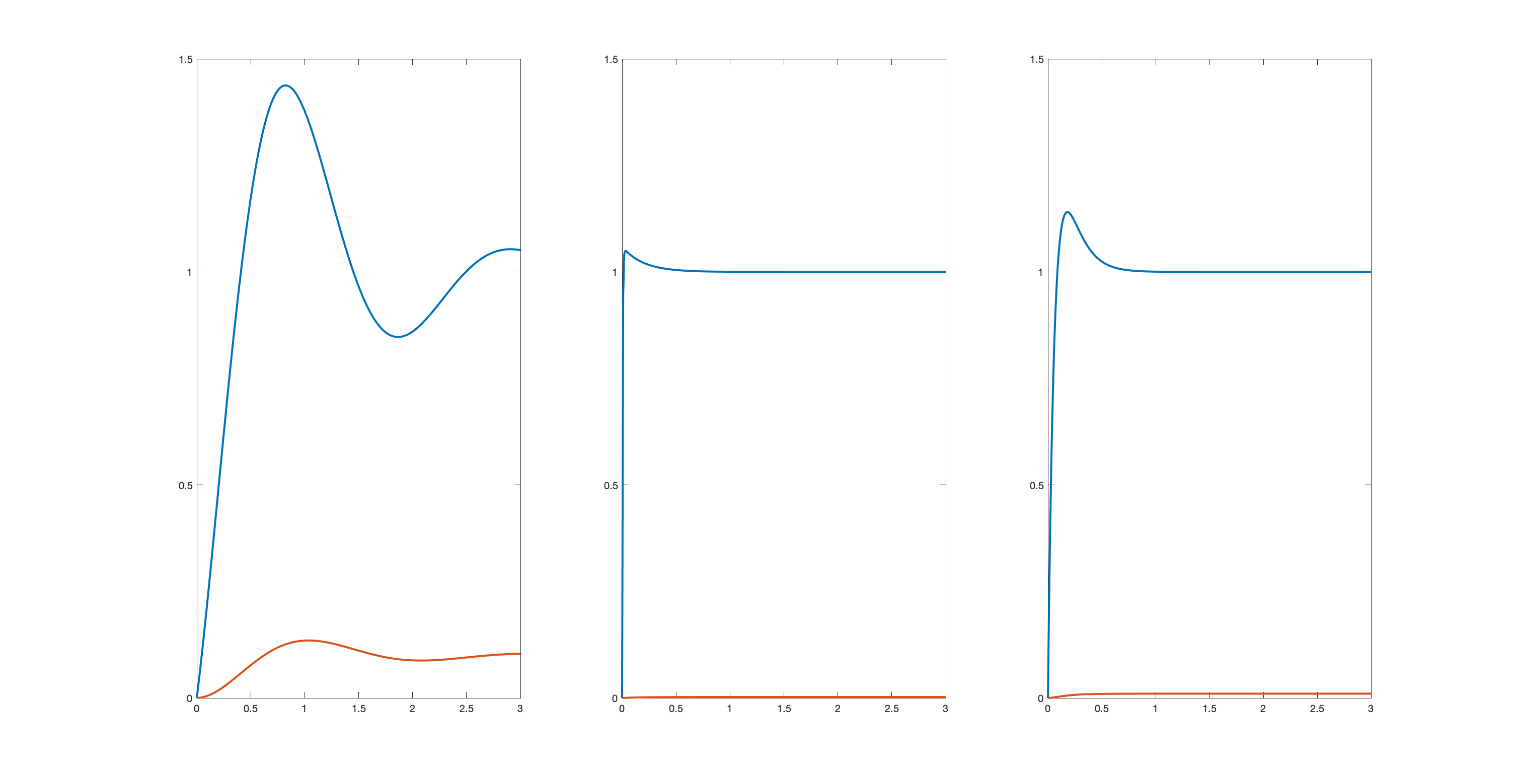
For the questions below, we will be analyzing the behavior of the PD control system of section 1 for three different sets of feedback gains. For the cases we will analyze, we will use \Delta T = 0.01, K_p = 10 K_0, and K_d = 2 K_0, where K_0 is a gain scaling factor. We will consider three cases, K_0 = 1, K_0 = 10, and K_0 = 45, whose three step responses are plotted below (NOT RESPECTIVELY!). The plots in blue are the responses to a unit step in the input, \theta_d, the plots in red are the responses to a unit step in the disturbance, \alpha_{dist}.
Using partial fraction expansion, we've seen that the step response for a system with two natural frequencies, assuming they are different from each other and different from 1, will be of the form
where \lambda_1, \lambda_2, are the natural frequencies, and \alpha_1, \alpha_2, and \alpha_{in} can be determined by partial fraction expansion. In addition, if the natural frequencies are all less than one in magnitude (the system is stable), then
for all i, and
Use your formulas for the disturbance transfer function, to determine the answers to the questions below.
What is the steady-state value for the disturbance step response for the system with the best disturbance rejection?
What is the maximum magnitude natural frequency for the system whose maximum magnitude natural frequency is smallest?
What is the maximum magnitude natural frequency for the system whose maximum magnitude natural frequency is largest?
For the system with the fastest settling step response, what is the value of \alpha_i for the natural frequency with the maximum magnitude?
**Clarification: You may approach this problem in several ways. (1) Computing the partial fraction decomposition of G(z)X(z) where X(z) is the z-transform of the unit step \frac{1}{1-z^{-1}} by hand (see the week 3 scribbles here and here) or (2) figure out how to use Matlab's residuez function. If you decide to use matlab's residuez function, you will need the numerator and denominator coefficients of G(z)X(z).
What you should have noticed from this problem is that the system with the highest K_0 (K_0 = 45) had the best disturbance rejection and the fastest settling time, but did NOT have the smallest maximum magnitude natural frequency. The reason the K_0=45 system settled faster even though one of its natural frequencies was larger than the K_0 = 10 case was because of a very small \alpha_i. So, natural frequencies tell you a LOT, but not everything!